Решение: Два моля идеального газа совершают замкнутый цикл, изображенный на рисунке

Условие задачи:

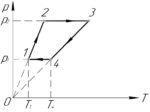Два моля идеального газа совершают замкнутый цикл, изображенный на рисунке. Известно, что температура \(T_1=280\) К, \(\frac{p_2}{p_1}=5\), \(\frac{T_4}{T_1}=2\). Чему равна работа, совершаемая газом за цикл?

Задача №5.5.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=2\) моль, \(T_1=280\) К, \(\frac{p_2}{p_1}=5\), \(\frac{T_4}{T_1}=2\), \(A-?\)

Решение задачи:

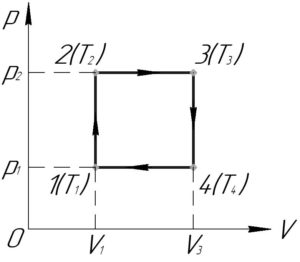Перестроим цикл, приведенный в условии в координатах p-T, в координатах p-V (смотрите схему к решению).

Работа газа за цикл \(A\) равна сумме работ газа в каждом из процессов, из которых состоит цикл. Работа газа в процессе численно равна площади фигуры под графиком процесса в координатах p-V, поэтому работа газа в процессах 1-2 и 3-4 равна нулю. Тогда:

\[A = {A_{23}} + {A_{41}}\;\;\;\;(1)\]

Работу газа \(A_{23}\) и \(A_{41}\) в изобарных процессах 2-3 и 4-1 найдём по таким известным формулам:

\[\left\{ \begin{gathered}
{A_{23}} = {p_2}\left( {{V_3} — {V_1}} \right) = {p_2}{V_3} — {p_2}{V_1} \hfill \\
{A_{41}} = {p_1}\left( {{V_1} — {V_3}} \right) = {p_1}{V_1} — {p_1}{V_3} \hfill \\
\end{gathered} \right.\]

Запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1-4:

\[\left\{ \begin{gathered}
{p_1}{V_1} = \nu R{T_1} \hfill \\
{p_2}{V_1} = \nu R{T_2} \hfill \\
{p_2}{V_3} = \nu R{T_3} \hfill \\
{p_1}{V_3} = \nu R{T_4} \hfill \\
\end{gathered} \right.\]

Тогда:

\[\left\{ \begin{gathered}
{A_{23}} = \nu R\left( {{T_3} — {T_2}} \right) \hfill \\
{A_{41}} = \nu R\left( {{T_1} — {T_4}} \right) \hfill \\
\end{gathered} \right.\]

Таким образом, формула (1) примет вид:

\[A = \nu R\left( {{T_3} — {T_2}} \right) + \nu R\left( {{T_1} — {T_4}} \right)\]

\[A = \nu R\left( {{T_3} — {T_2} + {T_1} — {T_4}} \right)\;\;\;\;(2)\]

Теперь все неизвестные температуры нужно выразить через известную температуру \(T_{1}\).

Процесс 1-2 — изохорный (\(V=const\)), запишем закон Шарля:

\[\frac{{{p_2}}}{{{T_2}}} = \frac{{{p_1}}}{{{T_1}}}\]

\[{T_2} = {T_1}\frac{{{p_2}}}{{{p_1}}}\]

Из условия задачи следует, что \(\frac{p_2}{p_1}=5\), поэтому:

\[{T_2} = 5{T_1}\;\;\;\;(3)\]

Аналогично, процесс 3-4 — изохорный (\(V=const\)), также запишем закон Шарля:

\[\frac{{{p_1}}}{{{T_4}}} = \frac{{{p_2}}}{{{T_3}}}\]

\[{T_3} = {T_4}\frac{{{p_2}}}{{{p_1}}}\]