Условие задачи:
В цилиндрический сосуд с водой, с площадью дна 150 см2, опускают тело массой 1 кг, с плотностью 800 кг/м3 (вода – 1000 кг/м3) и площадью горизонтального сечения 50 см2. Вода при этом из сосуда не выливается. Найти изменение уровня воды в сосуде.
Задача №3.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=150\) см2, \(m=1\) кг, \(\rho=800\) кг/м3, \(\rho_{в}\) кг/м3, \(S_1=50\) см2, \(h-?\)
Решение задачи:
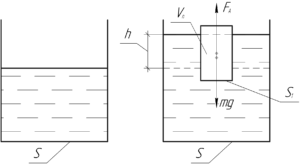Поскольку плотность материала \(\rho\), из которого изготовлено тело, меньше, чем плотность воды, значит тело плавает, погрузившись частично в воду. К такому выводу можно прийти, если предположить, что тело плавает, и записать условие плавания тел:
\[{F_А} = mg\;\;\;\;(1)\]
Распишем силу Архимеда \(F_А\) в левой части и массу \(m\) в правой, тогда получим такое равенство:
\[{\rho _в}g{V_п} = \rho Vg\]
\[{\rho _в}{V_п} = \rho V\]
Так как из условия понятно, что \(\rho_{в} > \rho\), значит \(V_{п} < V\), то есть мы доказали наше суждение выше.
Известно, что тело вытесняет объем воды, равный объему погруженной части тела. Значит справедливо равенство:
\[Sh = {V_п}\]
\[h = \frac{{{V_п}}}{S}\]
Объем погруженной части тела можно узнать из равенства (1), предварительно расписав в левой части силу Архимеда:
\[{\rho _в}g{V_п} = mg\]
\[{V_п} = \frac{m}{{{\rho _в}}}\]
В итоге искомое изменение уровня воды \(h\) найдем по формуле:
\[h = \frac{m}{{{\rho _в}S}}\]
Переведем площадь дна сосуда \(S\) в систему СИ и произведем вычисления:
\[150\;см^2 = 150 \cdot {10^{ – 4}}\;м^2\]
\[h = \frac{1}{{1000 \cdot 150 \cdot {{10}^{ – 4}}}} = 0,067\;м = 67\;мм\]
Ответ: 67 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.7 В стакане, наполненном до краев водой, плавает кусок льда. Как изменится давление
3.3.9 Вес куска железа в воде 1,67 Н. Найти его объем
3.3.10 Груз какой массы может поднять аэростат объемом 100000 м3 на высоту 40 км?
Надо доказать, что H xS =h x s. Это можно сделать так: Погрузим тело на глубину х, оно вытеснит объем s x (x). Эта вода займет объем между талом и стенками (S – s) x H, где Н – на сколько повысится уровень воды. Получим:
h x(x) = (S-s) x H, отсюда: SH = s(H + x), где (H + x) = h -глубина погружения тела. Получили: SH =sh. И теперь имеем: F(A) =Mg, pgsh= pgSH = Mg. отсюда находим Н.
Спасибо за комментарий, интересный подход к решению
Известно, что тело вытесняет объем воды, равный объему погруженной части тела. Значит справедливо равенство:
Sh=Vп
Вы пишите одно,а подставляете совсем другое.Площадь не та.
Доказываю, что все в решении написано верно.
Пусть начальная высота уровня воды равна H. Воду в сосуд мы не подливали, поэтому должно быть справедливо равенство:
SH = SH + Sh – Vп (смотрите рисунок к задаче)
Откуда Sh=Vп
Добрый день!
Зачем в условии задачи указывается площадь горизонтального сечения S1, если в решении это значение не используется?
Здравствуйте!
Такое встречается, и это абсолютно нормально.
Бывает, что авторы указывают в условии лишние данные, чтобы запутать решающих и внести сомнения в правильность решения. Иногда из одной задачи автор придумывает нескольких других, аналогичных, и забывает убрать некоторые данные.