Условие задачи:
В сосуде находятся две несмешивающиеся жидкости с различными плотностями. На границе раздела жидкостей плавает однородное тело объема \(V\). Плотность материала \(\rho\) больше плотности \(\rho_1\) верхней жидкости, но меньше плотности \(\rho_2\) нижней жидкости (\(\rho_1 < \rho< \rho_2\)). Какая часть объема тела находится в нижней жидкости?
Задача №3.3.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V\), \(\rho_1\), \(\rho_2\), \(\rho_1 < \rho< \rho_2\), \(\frac{V_{2}}{V}-?\)
Решение задачи:
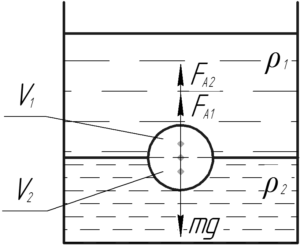Тело плавает на границе раздела жидкостей, запишем условие плавания тела:
\[{F_{А1}} + {F_{А2}} – mg = 0\]
Распишем силы Архимеда и массу, тогда получим:
\[{\rho _1}g{V_1} + {\rho _2}g{V_2} – \rho Vg = 0\]
\[{\rho _1}{V_1} + {\rho _2}{V_2} = \rho V\]
Поделим обе части на \(V\):
\[{\rho _1}\frac{{{V_1}}}{V} + {\rho _2}\frac{{{V_2}}}{V} = \rho \]
Так как тело погружено полностью в жидкости, то справедливо следующее равенство:
\[{V_1} + {V_2} = V\]
\[\frac{{{V_1}}}{V} + \frac{{{V_2}}}{V} = 1 \Rightarrow \frac{{{V_1}}}{V} = 1 – \frac{{{V_2}}}{V}\]
Тогда:
\[{\rho _1}\left( {1 – \frac{{{V_2}}}{V}} \right) + {\rho _2}\frac{{{V_2}}}{V} = \rho \]
\[{\rho _1} – {\rho _1}\frac{{{V_2}}}{V} + {\rho _2}\frac{{{V_2}}}{V} = \rho \]
\[\frac{{{V_2}}}{V} = \frac{{\rho – {\rho _1}}}{{{\rho _2} – {\rho _1}}}\]
Ответ: \(\frac{\rho – \rho _1}{\rho _2 – \rho _1}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.51 Два деревянных шара одинакового объема, полностью находящиеся в жидкости
3.3.53 Плотность воды 1000 кг/м3, а плотность пробки 200 кг/м3. Пробковый шар массы 100 г
3.3.54 Плотность воды 1000 кг/м3, а плотность камня 2500 кг/м3. Если не учитывать
