В одном из двух одинаковых заполненных водой сообщающихся сосудов плавает шарик

Условие задачи:

В одном из двух одинаковых заполненных водой сообщающихся сосудов плавает шарик массой 100 г. Сечение каждого сосуда 2 см². На сколько изменится уровень воды, если вынуть шарик?

Задача №3.1.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=100\) г, \(S=2\) см², \(\Delta h-?\)

Решение задачи:

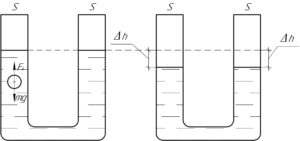Шарик, помещенный в один из сосудов, выдавит воду в объеме \(V_в\), равном объему шарика \(V_ш\), то есть:

\[{V_ш} = {V_в}\;\;\;\;(1)\]

Поскольку сосуды сообщающиеся, то уровень воды (при погружении шарика) поднимется в обоих сосудах. Если вынуть шарик, то жидкость в левом и правом сосуде опустится на высоту \(\Delta h\). Эту искомую величину следует искать из следующего соотношения:

\[{V_в} = 2S\Delta h\;\;\;\;(2)\]

Если шарик плавает, значит действующая на него сила Архимеда равна силе тяжести (условие плавания тел):

\[{F_А} = mg\]

Распишем в левой части силу Архимеда по известной формуле, тогда:

\[{\rho _в}g{V_ш} = mg\]

Сократив в обоих части на \(g\), получим:

\[m = {\rho _в}{V_ш}\]

\[{V_ш} = \frac{m}{{{\rho _в}}}\;\;\;\;(3)\]

Подставим (2) и (3) в (1), тогда:

\[\frac{m}{{{\rho _в}}} = 2S\Delta h\]

Откуда получим решение задачи в общем виде, оно выглядит так:

\[\Delta h = \frac{m}{{2{\rho _в}S}}\]

Переведем данные задачи в систему СИ:

\[100\;г = 0,1\;кг\]

\[2\;см^2 = 2 \cdot {10^{ – 4}}\;м^2\]

Считаем ответ (плотность воды равна \(\rho_{в}=1000\) кг/м³):

\[\Delta h = \frac{{0,1}}{{2 \cdot 1000 \cdot 2 \cdot {{10}^{ – 4}}}} = 0,25\;м\]

Ответ: 0,25 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.35 В две сообщающиеся трубки разного сечения налили сначала ртуть, а потом в широкую
3.1.37 В сосуд с водой вставлена трубка сечением 2 см2. В трубку налили 72 г масла. Найти
3.1.38 В колено U-образной трубки площадью 1 см2, содержащей ртуть, налили 7,2 г воды