Решение: Цилиндр высотой 40 см плавает в вертикальном положении в сосуде с водой. Определить

Условие задачи:

Цилиндр высотой 40 см плавает в вертикальном положении в сосуде с водой. Определить высоту погруженной части цилиндра, если его плотность 800 кг/м³.

Задача №3.3.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=40\) см, \(\rho=800\) кг/м³, \(h_{п}-?\)

Решение задачи:

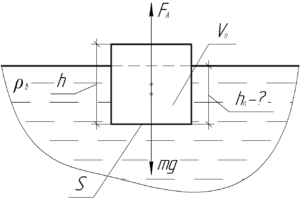Поскольку цилиндр плавает, то можно записать условие плавания тел:

\[{F_А} = mg\;\;\;\;(1)\]

Силу Архимеда находят по следующей формуле, где \(\rho_{в}\) — плотность жидкость, в которое погружено тело (в нашем случае — воды), \(g\) — ускорение свободного падения, \(V_{п}\) — объем погруженной части цилиндра. Последний можно найти как произведение площади основания цилиндра \(S\) на высоту погруженной части \(h_{п}\).

\[{F_А} = {\rho _в}g{V_п} = {\rho _в}gS{h_п}\]

Массу цилиндра \(m\) найдем как произведение плотности материала цилиндра \(\rho\) на полный объем \(V\) (который также можно найти через площадь \(S\) и высоту цилиндра \(h\)).

\[m = \rho V = \rho Sh\]

Равенство (1) примет такой вид:

\[{\rho _в}gS{h_п} = \rho Shg\]

\[{\rho _в}{h_п} = \rho h\]

Откуда высота погруженной в воду части цилиндра \(h_{п}\) равна:

\[{h_п} = \frac{\rho }{{{\rho _в}}}h\]

Плотность воды \(\rho_{в}\) равна 1000 кг/м³. Переведем высоту цилиндра в метры и посчитаем ответ:

\[40\;см = \frac{{40}}{{100}}\;м = 0,4\;м\]

\[{h_п} = \frac{{800}}{{1000}} \cdot 0,4 = 0,32\;м\]