Условие задачи:

Шарик плавает в сосуде, в котором находятся вода и масло. При этом 2/3 объема шарика находится в воде, а 1/3 — в масле. Найдите плотность материала, из которого сделан шарик.

Задача №3.3.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_в=\frac{2}{3}V\), \(V_м=\frac{1}{3}V\), \(\rho-?\)

Решение задачи:

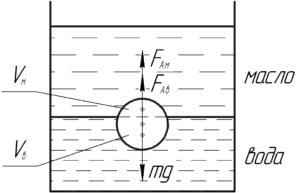На часть шарика, которая находится в воде, действует сила Архимеда \(F_{Ав}\), а которая находится в масле — сила Архимеда \(F_{Ам}\). На весь шарик также действует сила тяжести \(mg\). Поскольку шарик находится в равновесии, значит справедливо следующее равенство (первый закон Ньютона):

\[{F_{Ав}} + {F_{Ам}} = mg\;\;\;\;(1)\]

Распишем силу Архимеда для обеих частей шарика:

\[\left\{ \begin{gathered}
{F_{Ав}} = {\rho _в}g{V_в} = \frac{2}{3}{\rho _в}gV \hfill \\
{F_{Ам}} = {\rho _м}g{V_м} = \frac{1}{3}{\rho _м}gV \hfill \\
\end{gathered} \right.\]

Массу шарика можно найти через плотность его материала \(\rho\) и полный объем \(V\):

\[m = \rho V\]

С учетом вышесказанного равенство (1) примет вид:

\[\frac{2}{3}{\rho _в}gV + \frac{1}{3}{\rho _м}gV = \rho Vg\]

В итоге искомую плотность материала шарика \(\rho\) найдем по такой формуле:

\[\rho  = \frac{2}{3}{\rho _в} + \frac{1}{3}{\rho _м}\]

Плотности воды и масла — это табличные величины, равные соответственно 1000 кг/м³ и 910 кг/м³. Считаем ответ:

\[\rho  = \frac{2}{3} \cdot 1000 + \frac{1}{3} \cdot 910 = 970\;кг/м^3\]

Ответ: 970 кг/м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.19 Пробковый спасательный круг имеет массу 3,2 кг. Определить подъемную силу
3.3.21 Вес тела в воде в 5 раз меньше, чем в воздухе. Какова плотность вещества тела?
3.3.22 Льдина равномерной толщины, плавает в воде, выступая над её поверхностью на 2 см