Условие задачи:
Шар массой 6 кг висит на веревке, прикрепленной к гладкой стене. С какой силой шар давит на стенку, если веревка проходит через центр шара, а \(\alpha=30^\circ\)?
Задача №3.1.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=6\) кг, \(\alpha=30^\circ\), \(F-?\)
Решение задачи:
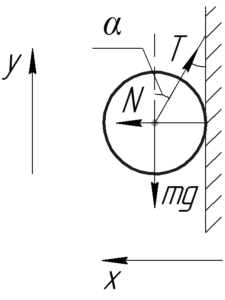Искомая сила давления шара на стенку \(F\) равна (по величине) силе реакции опоры \(N\) по третьему закону Ньютона.
Шар находится в равновесии под действием трёх сил: силы тяжести \(mg\), силы реакции опоры \(N\) и силы натяжения нити \(T\). Запишем первое условие равновесия в проекции на оси \(x\) и \(y\):
\[\left\{ \begin{gathered}
T \cdot \cos \alpha = mg \hfill \\
T \cdot \sin \alpha = N \hfill \\
\end{gathered} \right.\]
Нижнее равенство делим на верхнее, получим:
\[tg\alpha = \frac{N}{{mg}}\]
\[N = mg \cdot tg\alpha \]
Как было уже сказано \(F=N\), поэтому:
\[F = mg \cdot tg\alpha \]
Посчитаем ответ:
\[F = 6 \cdot 10 \cdot tg30^\circ = 34,6\;Н\]
Ответ: 34,6 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.4 Какую силу необходимо приложить, чтобы приподнять за один конец бревно
3.1.6 На обод колеса вагона действует тормозящая сила 500 Н. Определить момент этой силы
3.1.7 Два одинаковых шарика, масса и радиусы которых равны соответственно 100 г и 3 см
Добрый день, а почему мы делим нижнее равенство на верхнее?
Вам нужно из полученной системы уравнений найти \(N\). Как Вы это сделаете, абсолютно неважно, я пошёл таким путем (разделил нижнее уравнение на верхнее) , Вы можете пойти совершенно другим.
как найти силу натижения нити?
Смотрите систему уравнений, из первого из них можно сразу найти силу натяжения нити:\[T \cdot \cos \alpha = mg \Rightarrow T = \frac{{mg}}{{\cos \alpha }}\]\[T = \frac{{6 \cdot 10}}{{\cos 30^\circ }} = 69,3\;Н\]
tg30°= на что равно пожалуйста скажите
tg 30° равен корню из 3, делённому на 3
На будущее : посмотри таблицу Брадиса.
Это табличное значение