Решение: Подъемное устройство состоит из однородного стержня длиной L=2,5 м и массой m=5 кг

Условие задачи:

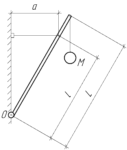Подъемное устройство состоит из однородного стержня длиной \(L=2,5\) м и массой \(m=5\) кг. Нижним концом O стержень шарнирно соединен со стеной, образуя с ней постоянный угол благодаря горизонтальному тросу, соединенному со стержнем на расстоянии \(l=2\) м от шарнира. Длина троса \(a=1\) м. Груз массой \(M=50\) кг подвешен в верхней точке стержня. Найдите натяжение троса.

Задача №3.1.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=2,5\) м, \(m=5\) кг, \(l=2\) м, \(a=1\) м, \(M=50\) кг, \(T-?\)

Решение задачи:

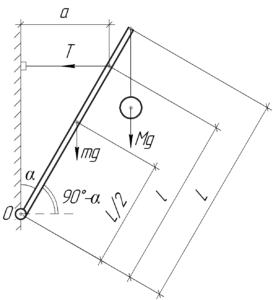На стержень действуют следующие силы: сила тяжести самого стержня \(mg\), сила тяжести груза \(Mg\), сила натяжения нити \(T\) и сила реакции в шарнире \(N\) (точка O).

Стержень находится в равновесии. Чтобы найти силу натяжения \(T\) достаточно записать правило моментов относительно точки O (второе условие равновесия) – момент силы реакции \(N\) относительно этой точки равен нулю.

\[T \cdot l \cdot \cos \alpha – Mg \cdot L \cdot \cos \left( {90^\circ – \alpha } \right) – mg \cdot \frac{L}{2} \cdot \cos \left( {90^\circ – \alpha } \right) = 0\]

Из тригонометрии известно, что \(\sin \alpha = \cos \left( {90^\circ – \alpha } \right)\), поэтому:

\[T \cdot l \cdot \cos \alpha – Mg \cdot L \cdot \sin \alpha – mg \cdot \frac{L}{2} \cdot \sin \alpha = 0\]

\[T \cdot l \cdot \cos \alpha = \frac{{gL}}{2} \cdot \sin \alpha \left( {2M + m} \right)\]

\[T = \frac{{\left( {2M + m} \right)gL \cdot tg\alpha }}{{2l}}\]

На схеме видно, что тангенс угла \(\alpha\) равен:

\[tg\alpha = \frac{a}{{\sqrt {{l^2} – {a^2}} }}\]

В итоге получим следующее решение этой задачи:

\[T = \frac{{\left( {2M + m} \right)gLa}}{{2l\sqrt {{l^2} – {a^2}} }}\]

Осталось только посчитать ответ:

\[T = \frac{{\left( {2 \cdot 50 + 5} \right) \cdot 10 \cdot 2,5 \cdot 1}}{{2 \cdot 2 \cdot \sqrt {{2^2} – {1^2}} }} = 379\;Н = 0,379\;кН\]