Условие задачи:
Под каким наименьшим углом \(\alpha\) к горизонту может стоять лестница, прислоненная к гладкой вертикальной стене, если коэффициент трения лестницы о пол равен \(\mu\)? Считать, что центр тяжести находится в середине лестницы.
Задача №3.1.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\mu\), \(\alpha-?\)
Решение задачи:
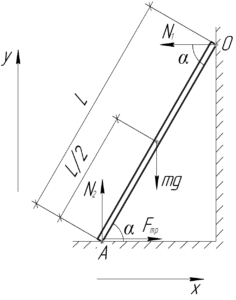Изобразим на схеме лестницу и все силы, приложенные к ней: силу тяжести \(mg\), силу нормальной реакции в точке O \(N_1\) и две компоненты силы реакции в точке A \(N_2\) и \(F_{тр}\).
Лестница находится в равновесии. Запишем первое условие равновесия в проекции на ось \(y\) (этого достаточно для решения задачи) и второе условие равновесия относительно точки O.
\[\left\{ \begin{gathered}
{N_2} = mg \;\;\;\;(1)\hfill \\
mg \cdot \frac{L}{2} \cdot \cos \alpha – {N_2} \cdot L \cdot \cos \alpha + {F_{тр}} \cdot L \cdot \sin \alpha = 0 \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Преобразуем равенство (2), чтобы выразить из него \(F_{тр}\):
\[\frac{{mg}}{2} – {N_2} + {F_{тр}} \cdot tg\alpha = 0\]
\[{F_{тр}} = \left( {{N_2} – \frac{{mg}}{2}} \right) \cdot ctg\alpha \]
Учтём равенство (1), тогда:
\[{F_{тр}} = \left( {{N_2} – \frac{{{N_2}}}{2}} \right) \cdot ctg\alpha = \frac{{{N_2}}}{2} \cdot ctg\alpha \]
Лестница будет оставаться в покое (нижний конец не будет проскальзывать), пока имеет место сила трения покоя, то есть выполняется неравенство:
\[{F_{тр}} \leq \mu {N_2}\]
Значит:
\[\frac{{{N_2}}}{2} \cdot ctg\alpha \leq \mu {N_2}\]
\[ctg\alpha \leq 2\mu \]
Ответ к этой задаче в сборнике указан через арктангенс, поэтому перейдем к тангенсу:
\[\frac{1}{{tg\alpha }} \leq 2\mu \]
\[tg\alpha \geq \frac{1}{{2\mu }}\]
\[\alpha \geq arctg\left( {\frac{1}{{2\mu }}} \right)\]
Минимальное значение угла \(\alpha\) соответствует случаю равенства, то есть:
\[{\alpha _{\min }} = arctg\left( {\frac{1}{{2\mu }}} \right)\]
Ответ: \(arctg\left( {\frac{1}{{2\mu }}} \right)\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.31 С помощью каната, перекинутого через неподвижный блок, укрепленный под потолком
3.1.33 Какой тормозящий момент относительно оси вращающегося колеса диаметра 40 см
3.1.34 На барабан лебедки диаметра 20 см намотан трос. К тросу подвесили груз массы 20 кг
А как вы так поменяли знак на противоположный в предпоследнем действии?
Вы про \(\frac{1}{{tg\alpha }} \leq 2\mu \)? Так умножьте обе части на \(tg\alpha\) и поделите на \(2\mu\) (кстати, оба этих выражения точно положительные, поэтому переживать не о чем)
из проекции сил на ось OX мы можем найти силу трения, она будет равна реакции 1 R1. но у нас не будет угла. Вы можете объяснить
А силу трения можно найти гораздо легче. Для случая, когда лестница стоит под минимальным углом:\[{F_{тр}} = \mu {N_2}\]Формула (1) решения:\[{N_2} = mg\]В итоге:\[{F_{тр}} = \mu mg\]
Она проще может быть решена, гораздо. Вообще задачи всей этой подборки (спасибо за нее!) я решила проще… А сборник очень хороший, благодаря Вам разжилась книжкой.
Каким же образом, откройте секрет
Люблю таких комментаторов, которые пишут, что задачу можно решить проще (причем гораздо проще!), но путь такого простого решения не описывают, даже в общих чертах (используемые законы, принципы, “фишки”, упрощения).
Не очень понятно 2 уравнение, по какому принципу расставляются моменты и их знаки. Почему мы взяли именно эти 3 величины?
Всего на лестницу действуют 4 силы, но момент силы N1 относительно точки O равен нулю (так как плечо этой силы относительно этой точки равно нулю), поэтому в уравнении моментов присутствуют лишь три другие силы.
Если сила “пытается” вращать тело относительно выбранной точки против часовой стрелки, то знак перед моментом будет “+”, иначе – “-“.