Надводная часть айсберга имеет объем 1000 м3. При какой плотности льда объем

Условие задачи:

Надводная часть айсберга имеет объем 1000 м³. При какой плотности льда объем подводной части будет равен 8000 м³?

Задача №3.3.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_н=1000\) м³, \(V_п=8000\) м³, \(\rho_л-?\)

Решение задачи:

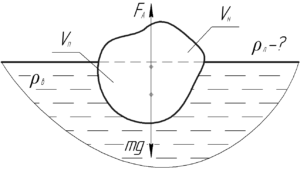Понятно, что айсберг плавает, поэтому запишем условие плавания тел, согласно которому сила Архимеда равна по величине силе тяжести:

\[{F_А} = mg\;\;\;\;(1)\]

Силу Архимеда \(F_А\) находят по следующей формуле, в которой \(\rho_в\) – это плотность воды (равная 1000 кг/м³):

\[{F_А} = {\rho _в}g{V_п}\;\;\;\;(2)\]

Если учесть, что полный объем айсберга \(V\) равен сумме объемов надводной \(V_н\) и подводной его части \(V_п\), то массу айсберга можно выразить следующим образом через плотность льда \(\rho_л\):

\[m = {\rho _л}V = {\rho _л}\left( {{V_н} + {V_п}} \right)\;\;\;\;(3)\]

Подставим выражения (2) и (3) в равенство (1):

\[{\rho _в}g{V_п} = {\rho _л}\left( {{V_н} + {V_п}} \right)g\]

\[{\rho _в}{V_п} = {\rho _л}\left( {{V_н} + {V_п}} \right)\]

Откуда искомая плотность льда \(\rho_л\) равна:

\[{\rho _л} = {\rho _в}\frac{{{V_п}}}{{{V_н} + V_п}}\]

Численное значение плотности льда равна:

\[{\rho _л} = 1000 \cdot \frac{{8000}}{{8000 + 1000}} = 889\;кг/м^3\]

Ответ: 889 кг/м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.17 На плоту, состоящем из 20 одинаковых бревен, можно перевозить груз максимальной
3.3.19 Пробковый спасательный круг имеет массу 3,2 кг. Определить подъемную силу
3.3.20 Шарик плавает в сосуде, в котором находятся вода и масло. При этом 2/3 объема