Условие задачи:

Каков должен быть коэффициент трения, чтобы заколоченный в бревно клин не выскакивал из него? Угол при вершине клина 30°. Массой клина пренебречь.

Задача №3.1.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\mu-?\)

Решение задачи:

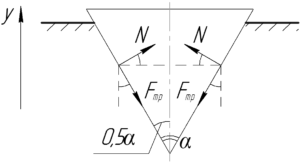На клин со стороны бревна, в которое и заколочен клин, действуют силы нормальной реакции опоры \(N\) и силы трения \(F_{тр}\). Обратите внимание, что соответствующие силы, действующие на правую и левую часть, одинаковы, так как схема симметрична.

Клин находится в равновесии, поэтому запишем первое условие равновесия в проекции на ось \(y\). Все необходимые для проецирования углы показаны на схеме:

\[2N \cdot \sin \frac{\alpha }{2} — 2{F_{тр}} \cdot \cos \frac{\alpha }{2} = 0\]

\[{F_{тр}} = N \cdot tg\frac{\alpha }{2}\;\;\;\;(1)\]

Клин не выскакивает («не выскальзывает») из бревна, если имеет место сила трения покоя, т.е. выполняется известное неравенство:

\[{F_{тр}} \leq \mu N\]

Поэтому:

\[N \cdot tg\frac{\alpha }{2} \leq \mu N\]

\[\mu  \geq tg\frac{\alpha }{2}\]

Посчитаем минимальный коэффициент трения, при котором клин не будет выскакивать:

\[{\mu _{\min }} = tg\frac{\alpha }{2}\]

\[{\mu _{\min }} = tg\frac{{30^\circ }}{2} = 0,27\]

Ответ: 0,27.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.19 На тело массой 2 кг, покоящееся на гладкой наклонной плоскости с углом при основании
3.1.21 К стене приставлена лестница массой 60 кг. Центр тяжести лестницы находится
3.1.22 Лестница массой 15 кг и длиной 3 м стоит, упираясь верхним концом в гладкую стену