Условие задачи:
Два одинаковых шарика, масса и радиусы которых равны соответственно 100 г и 3 см, подвешены на невесомых нитях длиной 4 см к одной и той же точке. Чему равна сила давления одного шарика на другой в состоянии покоя?
Задача №3.1.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=100\) г, \(R=3\) см, \(L=4\) см, \(F-?\)
Решение задачи:
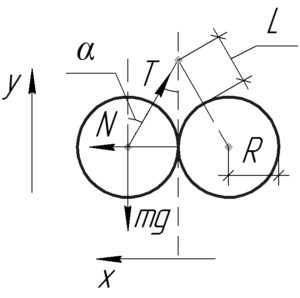Так как шарики одинаковые, то схема будет симметрична, поэтому достаточно рассмотреть силы, действующие только на один из них. По третьему закону Ньютона искомая сила давления \(F\) равна силе реакции \(N\).
\[F = N\;\;\;\;(1)\]
Запишем первое условие равновесия в проекции на обе оси для левого шарика:
\[\left\{ \begin{gathered}
T \cdot \cos \alpha = mg \hfill \\
T \cdot \sin \alpha = N \hfill \\
\end{gathered} \right.\]
Делим нижнее равенство системы на верхнее, тогда получим:
\[tg\alpha = \frac{N}{{mg}}\]
\[N = mg \cdot tg\alpha \]
Учитывая равенство (1), имеем:
\[F = mg \cdot tg\alpha \;\;\;\;(2)\]
Осталось только найти тангенс угла \(\alpha\). На схеме видно, что:
\[tg\alpha = \frac{R}{{\sqrt {{{\left( {L + R} \right)}^2} — {R^2}} }}\]
В числителе под корнем распишем разность квадратов:
\[tg\alpha = \frac{R}{{\sqrt {\left( {L + R — R} \right)\left( {L + R + R} \right)} }}\]
\[tg\alpha = \frac{R}{{\sqrt {L\left( {L + 2R} \right)} }}\]
Полученное подставим в формулу (2):
\[F = \frac{{mgR}}{{\sqrt {L\left( {L + 2R} \right)} }}\]
Переведем исходные данные задачи в систему СИ:
\[100\;г = \frac{{100}}{{1000}}\;кг = 0,1\;кг\]
\[3\;см = \frac{3}{{100}}\;м = 0,03\;м\]
\[4\;см = \frac{4}{{100}}\;м = 0,04\;м\]
Теперь считаем ответ:
\[F = \frac{{0,1 \cdot 10 \cdot 0,03}}{{\sqrt {0,04 \cdot \left( {0,04 + 2 \cdot 0,03} \right)} }} = 0,474\;Н = 474\;мН\]
Ответ: 474 мН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.6 На обод колеса вагона действует тормозящая сила 500 Н. Определить момент этой силы
3.1.8 К тросу длиной 3 м, концы которого закреплены на одной высоте, на расстоянии 1 м
3.1.9 Шар массой 5 кг опирается на две гладкие плоскости, образующие угол, причем
можно как то разными цветами выделять силы? У вас все черным и нечего не понятно
Учтем на будущее
Здравствуйте!
Не совсем понял почему при нахождении тангенса угла, в знаменателе пишем L^2+R^2-R^2, откуда здесь + R^2?
Чтобы найти тангенс угла \(\alpha\), нам нужно противолежащий катет разделить на прилежащий. Противолежащий катет равен радиусу шарика \(R\), а вот прилежащий мы можем найти из теоремы Пифагора. При этом гипотенуза в прямоугольном треугольнике равна \(L + R\), т.е. сумме радиуса шарика и длины нити. Поэтому прилежащий катет по теореме Пифагора определяется так: \(\sqrt {{{\left( {L + R} \right)}^2} — {R^2}} \).
Спасибо за ответ! Но разве L — это не гипотенуза? А если нет, то почему гипотенуза равняется L + R?
Нет, смотрите на рисунок внимательно. \(L\) — это длина нити, \(R\) — радиус шарика, а гипотенуза в прямоугольном треугольнике равна \(L + R\).
А вот в чём дело! Спасибо, понял.
Добрый день!
Не понятно: как вы выразили tg угла через R и L?
Рассмотрите прямоугольный треугольник на схеме, тангенс указанного угла — это отношение противолежащего катета (который равен радиусу шара R) к прилежащему (этот катет можно найти из теоремы Пифагора).
Спасибо, разобрался.