Условие задачи:

Доска толщиной 5 см плавает в воде, погрузившись на 70%. Поверх воды разливается слой нефти толщиной 1 см. На сколько будет выступать доска над поверхностью нефти?

Задача №3.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(h=5\) см, \(\frac{V_{пв1}}{V}=0,7\), \(h_{н}=1\) см, \(a-?\)

Решение задачи:

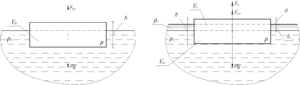Доска изначально плавает в воде, запишем условие плавания тел:

\[{F_{Ав1}} = mg\;\;\;\;(1)\]

Распишем по формуле силу Архимеда в левой части и массу (через плотность и объем) — в правой, тогда получим:

\[{\rho _в}g{V_{пв1}} = \rho Vg\]

\[{\rho _в}{V_{пв1}} = \rho V\]

По условию \(\frac{V_{пв1}}{V}=0,7\) (доска погружена в воду на 70%), поэтому плотность материала доски равна:

\[0,7{\rho _в}V = \rho V \Rightarrow \rho  = 0,7{\rho _в}\]

Плотность воды \(\rho_{в}\) равна 1000 кг/м³.

Далее поверх воды разливают нефть. Очевидно, она будет находиться выше, чем вода, поскольку имеет меньшую плотность (\(\rho_{н}=800\) кг/м³). Доска также будет плавать, запишем второй раз условие плавания тел:

\[{F_{Ав2}} + {F_{Ан}} = mg\;\;\;\;(2)\]

Если сравнить равенства (1) и (2), то видно, что у них равны правые части. Значит сила Архимеда \(F_{Ав1}\) в первом случае больше, чем \(F_{Ав2}\) во втором. Значит когда разольют нефть, объем доски, погруженный в воду, станет меньше.

Распишем равенство (2):

\[{\rho _в}g{V_{пв2}} + {\rho _н}g{V_{пн}} = \rho Vg\]

\[{\rho _в}{V_{пв2}} + {\rho _н}{V_{пн}} = \rho V\]

Доска имеет постоянное поперечное сечение площадью \(S\). Тогда понятно, что полный объем \(V\) равен \(Sh\), объем доски \(V_{пн}\), погруженный в нефть, равен \(Sh_{н}\). Если доска будет выступать над нефтью на величину \(a\), то объем доски \(V_{пв2}\), погруженный в воду, равен \(S\left( {h — {h_н} — a} \right)\) (смотрите схему).

\[{\rho _в}S\left( {h — {h_н} — a} \right) + {\rho _н}S{h_н} = \rho Sh\]

\[{\rho _в}\left( {h — {h_н} — a} \right) + {\rho _н}{h_н} = \rho h\]

Ранее мы выяснили, что \(\rho  = 0,7{\rho _в}\), поэтому:

\[{\rho _в}\left( {h — {h_н} — a} \right) + {\rho _н}{h_н} = 0,7{\rho _в}h\]

Осталось только выразить искомую величину \(a\):

\[{\rho _в}h — {\rho _в}{h_н} — {\rho _в}a + {\rho _н}{h_н} = 0,7{\rho _в}h\]

\[0,3{\rho _в}h — {\rho _в}{h_н} + {\rho _н}{h_н} = {\rho _в}a\]

\[a = 0,3h — {h_н}\left( {1 — \frac{{{\rho _н}}}{{{\rho _в}}}} \right)\]

Переведем некоторые величины в систему СИ и посчитаем ответ:

\[5\;см = 0,05\;м\]

\[1\;см = 0,01\;м\]

\[a = 0,3 \cdot 0,05 — 0,01 \cdot \left( {1 — \frac{{800}}{{1000}}} \right) = 0,013\;м = 13\;мм\]

Ответ: 13 мм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.23 Из воды с глубины 5 м поднимают на поверхность камень объемом 0,6 м3. Плотность
3.3.25 Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку
3.3.26 Плотность жидкости в 3 раза больше плотности материала тела. Какая часть объема