Условие задачи:
Брусок дерева плавает в воде. Объем погруженной части бруска 36 см3. Определить массу бруска.
Задача №3.3.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_{п}=36\) см3, \(m-?\)
Решение задачи:
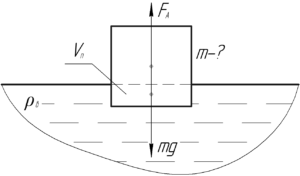Если брусок плавает, значит сила Архимеда \(F_{А}\) равна по величине силе тяжести \(mg\).
\[{F_А} = mg\;\;\;\;(1)\]
Силу Архимеда \(F_{А}\) определяют по следующей формуле, где \(\rho_{в}\) – плотность воды (жидкости, в которую погружен брусок), \(V_{п}\) – объем погруженной части.
\[{F_А} = {\rho _в}g{V_п}\]
Тогда равенство (1) станет таким:
\[{\rho _в}g{V_п} = mg\]
Откуда искомую массу бруска \(m\) можно найти по формуле:
\[m = {\rho _в}{V_п}\]
Плотность воды равна 1000 кг/м3 (это табличная величина). Переведем объем погруженной части в систему СИ и посчитаем ответ:
\[36\;см^3 = 36 \cdot {10^{ – 6}}\;м^3\]
\[m = 1000 \cdot 36 \cdot {10^{ – 6}} = 0,036\;кг = 36\;г\]
Ответ: 36 г.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.1 В воде плавает шар, погрузившись на 0,25 своего объема. Определить плотность
3.3.3 Льдина плавает на поверхности воды. Часть её объема, равная 150 м3, находится
3.3.4 На тело, находящееся в воде, действует выталкивающая сила 2 Н. С какой силой это тело