Условие задачи:

Аквариум имеет форму куба со стороной 0,6 м. До какой высоты следует налить в него воду, чтобы сила давления на боковую стенку была в 6 раз меньше, чем на дно? Атмосферное давление не учитывать.

Задача №3.2.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(a=0,6\) м, \(P_{д}=6P_{ст}\), \(h-?\)

Решение задачи:

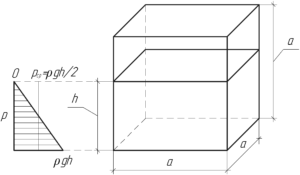Давление воды на уровне дна аквариума можно найти по формуле:

\[p_д = \rho gh\]

Площадь дна аквариума найдем по формуле (смотрите схему):

\[{S_д} = {a^2}\]

Тогда сила давления воды на дно \(P_{д}\) равно:

\[{P_д} = {p_д}{S_д} = \rho gh{a^2}\]

Давление воды на уровне поверхности равно нулю, а на уровне дна — \( \rho gh\). Так как давление зависит линейно от глубины, то среднее давление на стенку аквариума равно:

\[{p_{ст}} = \rho g\frac{h}{2}\]

Площадь соприкосновения воды на боковой стенке определим по формуле:

\[{S_{ст}} = ah\]

Тогда сила давления воды на стенку \(P_{ст}\) равна:

\[{P_{ст}} = {p_{ст}}{S_{ст}} = \rho g\frac{h}{2}ah\]

По условию \(P_{д}=6P_{ст}\), поэтому:

\[\rho gh{a^2} = 6 \cdot \frac{1}{2}\rho ghah\]

\[{a^2} = 3ah\]

\[h = \frac{a}{3}\]

Высота воды в аквариуме равна:

\[h = \frac{{0,6}}{3} = 0,2\;м\]

Ответ: 0,2 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.2.3 В сосуд налито воды высотой 20 см. Определить среднее давление воды на стенку
3.2.5 Аквариум наполнен доверху водой. С какой средней силой давит вода на стенку
3.2.6 В сосуд, имеющий форму прямоугольной призмы, шириной 15 см и длиной 35 см налита