Условие задачи:
К амперметру с внутренним сопротивлением 0,03 Ом подключен медный шунт длиной 10 см и сечением 1,7 мм2. Какой максимальный ток можно измерить этим амперметром, если он рассчитан на силу тока 0,4 А?
Задача №7.5.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_А=0,03\) Ом, \(L=10\) см, \(S=1,7\) мм2, \(I_0=0,4\) А, \(I-?\)
Решение задачи:
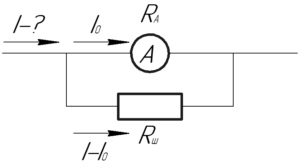 Для измерения силы тока на каком-либо участке электрической цепи используют амперметр, его располагают на том участке, где и нужно измерить величину силы тока. Если предел измерения амперметра (т.е. максимальное значение силы тока, которое может измерить амперметр) не позволяет измерить силу тока на этом участке, то к амперметру параллельно подключают шунт сопротивлением \(R_{ш}\). Шунт уменьшает силу тока на амперметре.
Для измерения силы тока на каком-либо участке электрической цепи используют амперметр, его располагают на том участке, где и нужно измерить величину силы тока. Если предел измерения амперметра (т.е. максимальное значение силы тока, которое может измерить амперметр) не позволяет измерить силу тока на этом участке, то к амперметру параллельно подключают шунт сопротивлением \(R_{ш}\). Шунт уменьшает силу тока на амперметре.
Так как амперметр и шунт соединены параллельно, то на них одинаковое напряжение \(U\). Сила тока на амперметре не должна превышать предела измерения \(I_0\), тогда на шунте сила тока будет равна \(\left( {I — {I_0}} \right)\). Здесь \(I\) — сила тока на том участке, где нужно произвести измерение. Поэтому:
\[\left\{ \begin{gathered}
U = {I_0}{R_А} \hfill \\
U = \left( {I — {I_0}} \right){R_ш} \hfill \\
\end{gathered} \right.\]
Тогда, очевидно, имеем:
\[{I_0}{R_А} = \left( {I — {I_0}} \right){R_ш}\]
Раскроем скобки в правой части равенства:
\[{I_0}{R_А} = I{R_ш} — {I_0}{R_ш}\]
\[{I_0}{R_А} + {I_0}{R_ш} = I{R_ш}\]
\[{I_0}\left( {{R_А} + {R_ш}} \right) = I{R_ш}\]
В итоге получим такую формулу для расчета силы тока \(I\):
\[I = {I_0}\frac{{{R_А} + {R_ш}}}{{{R_ш}}}\]
\[I = {I_0}\left( {\frac{{{R_А}}}{{{R_ш}}} + 1} \right)\]
Сопротивление шунта \(R_ш\) легко определить по такой формуле (здесь \(\rho\) — удельное электрическое сопротивление меди, равное 17 нОм·м):
\[{R_ш} = \rho \frac{L}{S}\]
Окончательно имеем такое решение задачи в общем виде:
\[I = {I_0}\left( {\frac{{{R_А}S}}{{\rho L}} + 1} \right)\]
Подставим численные данные задачи в эту формулу и посчитаем ответ:
\[I = 0,4 \cdot \left( {\frac{{0,03 \cdot 1,7 \cdot {{10}^{ — 6}}}}{{17 \cdot {{10}^{ — 9}} \cdot 0,1}} + 1} \right) = 12,4\;А\]
Ответ: 12,4 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.15 Гальванометр со шкалой из 100 делений и ценой деления 50 мкА/дел, надо использовать как
7.5.17 Предел измерения амперметра 5 А, число делений шкалы 100, внутреннее сопротивление
7.5.18 Вольтметр, внутреннее сопротивление которого 50 кОм, подключенный к источнику