Условие задачи:
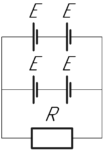Четыре одинаковых источника тока соединены, как показано на рисунке. ЭДС каждого источника равна 3 В, внутреннее сопротивление 0,5 Ом. Определите мощность, выделяющуюся на внешнем сопротивлении \(R=2\) Ом.
Задача №7.4.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\rm E_0=3\) В, \(r_0=0,5\) Ом, \(R=2\) Ом, \(P-?\)
Решение задачи:
Мощность \(P\), выделяющуюся на внешнем сопротивлении \(R\), будем определять по следующей формуле:
\[P = {I^2}R\]
Силу тока на внешнем сопротивлении \(R\) будем определять по закону Ома для полной цепи:
\[I = \frac{{\rm E}}{{R + r}}\]
Тогда:
\[P = \frac{{{{\rm E}^2}R}}{{{{\left( {R + r} \right)}^2}}}\;\;\;\;(1)\]
В этой формуле \(\rm E\) — это эквивалентная ЭДС, а \(r\) — это эквивалентное внутреннее сопротивление батареи источников, указанных на схеме.
Сначала найдем эквивалентную ЭДС \(\rm E_1\) и эквивалентное внутреннее сопротивление \(r_1\) источников, соединённых последовательно (т.е. источников на одной ветви). Это можно сделать по следующим формулам:
\[\left\{ \begin{gathered}
{{\rm E}_1} = 2{{\rm E}_0} \hfill \\
{r_1} = 2{r_0} \hfill \\
\end{gathered} \right.\]
Теперь найдем эквивалентную ЭДС \(\rm E\) и эквивалентное внутреннее сопротивление \(r\) двух параллельно соединенных эквивалентных ЭДС:
\[\left\{ \begin{gathered}
{\rm E} = {{\rm E}_1} \hfill \\
r = \frac{{{r_1}}}{2} \hfill \\
\end{gathered} \right.\]
Учитывая ранее приведенную систему, имеем:
\[\left\{ \begin{gathered}
{\rm E} = 2{{\rm E}_0} \hfill \\
r = {r_0} \hfill \\
\end{gathered} \right.\]
Значит формула (1) примет вид:
\[P = \frac{{4{\rm E}_0^2R}}{{{{\left( {R + {r_0}} \right)}^2}}}\]
Отлично, задача решена в общем виде. Подставим численные значения величин в формулу и посчитаем численный ответ задачи:
\[P = \frac{{4 \cdot {3^2} \cdot 2}}{{{{\left( {2 + 0,5} \right)}^2}}} = 11,52\;Вт\]
Ответ: 11,52 Вт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.4.33 Скоростной лифт массой 1600 кг за 300 с поднимается на высоту 30 м. Определить силу тока
7.4.35 На сколько градусов поднимется температура медного стержня, если по нему в течение 0,5 с
7.4.36 Определить ток короткого замыкания источника питания, если при токе 15 А он отдает