Воздушный шар имеет легкорастяжимую теплоизолированную оболочку массой 130 кг

Условие задачи:

Воздушный шар имеет легкорастяжимую теплоизолированную оболочку массой 130 кг, которая была заполнена 65 кг воздуха при атмосферных давлении и температуре. На сколько градусов нужно нагреть воздух внутри шара, чтобы он взлетел? Температура окружающей среды 0° C.

Задача №4.2.78 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m_{об}=130\) кг, \(m=65\) кг, \(t_0=0^\circ\) C, \(\Delta T-?\)

Решение задачи:

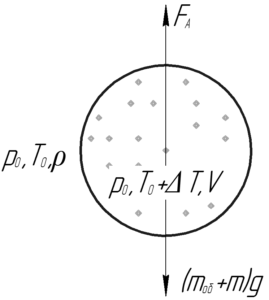Шар взлетит, когда сила Архимеда станет равной силе тяжести, т.е выполнится условие плавания тел:

\[{F_А} = \left( {{m_{об}} + m} \right)g\]

Выталкивающая сила \(F_А\) равна произведению плотности окружающего воздуха \(\rho\), ускорения свободного падения \(g\) и объема воздушного шара \(V\).

\[{F_А} = \rho gV\]

Поэтому:

\[\rho gV = \left( {{m_{об}} + m} \right)g\]

\[\rho V = {m_{об}} + m\;\;\;\;(1)\]

Теперь запишем уравнение Клапейрона-Менделеева для окружающего воздуха и воздуха внутри шара. Давление воздуха внутри шара равно давлению окружающего воздуха, т.е. атмосферному давлению \(p_0\), так как оболочка шара является легкорастяжимой.

\[\left\{ \begin{gathered}
{p_0}{V_1} = \frac{{{m_1}}}{M}R{T_0} \;\;\;\;(2)\hfill \\
{p_0}V = \frac{m}{M}R\left( {{T_0} + \Delta T} \right) \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Обе части уравнения (2) разделим на некоторый объем \(V_1\). Учитывая, что отношение массы \(m_1\) к объему \(V_1\) равно плотности окружающего воздуха \(\rho\), получим:

\[{p_0} = \frac{\rho }{M}R{T_0}\]

Выразим плотность окружающего воздуха \(\rho\):

\[\rho  = \frac{{{p_0}M}}{{R{T_0}}}\]

Из уравнения (3) выразим объем шара \(V\):

\[V = \frac{{mR\left( {{T_0} + \Delta T} \right)}}{{{p_0}M}}\]

Полученные выражения для плотности \(\rho\) и объема шара \(V\) подставим в формулу (1):

\[\frac{{{p_0}M}}{{R{T_0}}} \cdot \frac{{mR\left( {{T_0} + \Delta T} \right)}}{{{p_0}M}} = {m_{об}} + m\]

\[\frac{{m\left( {{T_0} + \Delta T} \right)}}{{{T_0}}} = {m_{об}} + m\]

\[m\left( {1 + \frac{{\Delta T}}{{{T_0}}}} \right) = {m_{об}} + m\]

\[m + m\frac{{\Delta T}}{{{T_0}}} = {m_{об}} + m\]

\[m\frac{{\Delta T}}{{{T_0}}} = {m_{об}}\]

\[\Delta T = {T_0}\frac{{{m_{об}}}}{m}\]

Переведем температуру в систему СИ:

\[0^\circ\;C  = 273\;К\]

Посчитаем ответ:

\[\Delta T = 273\frac{{130}}{{65}} = 546\;К = 546^\circ\;C \]

Помните, что изменение температуры выражается одним и тем же числом, что в шкале Кельвина, что в шкале Цельсия!

Ответ: 546° C.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.77 Насос захватывает при каждом качании 1 л воздуха при нормальных условиях и нагнетает
4.2.79 В некотором процессе давление и объем идеального газа связаны соотношением
4.2.80 Какой радиус должен иметь наполненный гелием воздушный шар, чтобы он мог подняться