Условие задачи:

В цилиндре с площадью основания 100 см² находится воздух. Поршень расположен на высоте 50 см от дна цилиндра. На поршень кладут груз массой 50 кг, при этом он опускается на 10 см. Найти температуру воздуха после опускания поршня, если первоначальное давление было равно 101 кПа, а температура 12° C.

Задача №4.2.100 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S=100\) см², \(h=50\) см, \(m=50\) кг, \(\Delta h=10\) см, \(p_1=101\) кПа, \(t_1=12^\circ\) C, \(T_2-?\)

Решение задачи:

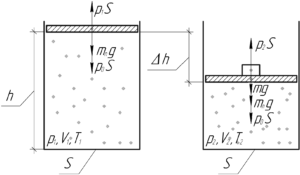Для начала запишем уравнение Клапейрона (объединённый газовый закон) для начального и конечного состояния воздуха в сосуде:

\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\]

Выразим из уравнения конечную температуру \(T_2\):

\[{T_2} = {T_1}\frac{{{p_2}{V_2}}}{{{p_1}{V_1}}}\;\;\;\;(1)\]

Объем, занимаемый газом в каждом состоянии, можно найти как произведение площади основания \(S\) на высоту, на которой находится поршень, поэтому:

\[\left\{ \begin{gathered}
{V_1} = Sh \hfill \\
{V_2} = S\left( {h — \Delta h} \right) \hfill \\
\end{gathered} \right.\]

Теперь разберемся с давлением. Запишем условие равновесия поршня (первый закон Ньютона) при начальном и конечном состоянии газа:

\[\left\{ \begin{gathered}
{p_1}S = {p_0}S + {m_п}g \hfill \\
{p_2}S = {p_0}S + {m_п}g + mg \hfill \\
\end{gathered} \right.\]

Здесь \(m_п\) — масса поршня, \(p_0\) — атмосферное давление. Видно, что имеет место равенство:

\[{p_2}S = {p_1}S + mg\]

Можно сделать вывод, что конечное давление \(p_2\) больше начального \(p_1\) на величину давления, которое создаёт груз, то есть:

\[{p_2} = {p_1} + \frac{{mg}}{S}\]

В итоге формула (1) примет такой вид:

\[{T_2} = {T_1}\frac{{\left( {{p_1} + \frac{{mg}}{S}} \right) \cdot S\left( {h — \Delta h} \right)}}{{{p_1} \cdot Sh}}\]

\[{T_2} = {T_1}\left( {1 + \frac{{mg}}{{{p_1}S}}} \right) \cdot \left( {1 — \frac{{\Delta h}}{h}} \right)\]

Мы решили задачу в общем виде. Выполним перевод некоторых единиц в систему СИ и посчитаем ответ:

\[100\;см^2 = 100 \cdot {10^{ — 4}}\;м^2\]

\[50\;см = 0,5\;м\]

\[10\;см = 0,1\;м\]

\[12^\circ\;C  = 285\;К\]

\[{T_2} = 285 \cdot \left( {1 + \frac{{50 \cdot 10}}{{101 \cdot {{10}^3} \cdot 100 \cdot {{10}^{ — 4}}}}} \right) \cdot \left( {1 — \frac{{0,1}}{{0,5}}} \right) = 340,87\;К = 67,87^\circ\;C \]

Ответ: 67,87° C.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.99 Воздушный шар объемом 1000 м3 наполнен гелием при температуре окружающего воздуха
4.2.101 В сосуд, на дне которого лежит твердый шар, нагнетают воздух при температуре 27 C
4.2.102 В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами