Решение: В цилиндре под поршнем находится воздух. Вес поршня 60 Н

Условие задачи:

В цилиндре под поршнем находится воздух. Вес поршня 60 Н, площадь сечения цилиндра 20 см², атмосферное давление 100 кПа. Груз какой массы надо положить на поршень, чтобы объем воздуха в цилиндре уменьшился в два раза при постоянной температуре?

Задача №4.3.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(P=60\) Н, \(S=20\) см², \(p_{атм}=100\) кПа, \(V_1=\frac{V_0}{2}\), \(m-?\)

Решение задачи:

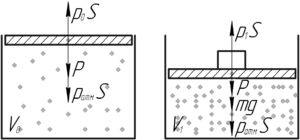Рисунок к задаче, на котором изображены все силы, действующие на поршень до и после установки груза, изображен справа.

Объем воздуха уменьшается при постоянной температуре, т.е. процесс изотермический (\(T = const\)), поэтому запишем закон Бойля-Мариотта, чтобы узнать как изменится давление:

\[{p_0}{V_0} = {p_1}{V_1}\]

Т.к. объем уменьшится в два раза, т.е. \(V_1=\frac{V_0}{2}\), то:

\[{p_0}{V_0} = {p_1}\frac{{{V_0}}}{2} \Rightarrow {p_1} = 2{p_0}\]

Поскольку поршень находится в начале и конце процесса в равновесии, то запишем первый закон Ньютона для этих случаев:

\[\left\{ \begin{gathered}
{p_0}S = P + {p_{атм}}S\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
{p_1}S = P + {p_{атм}}S + mg\,\,(2) \hfill \\
\end{gathered} \right.\]

Вычтем выражение (2) из (1) и выразим искомую массу груза \(m\):

\[m = \frac{{\left( {{p_1} — {p_0}} \right)S}}{g}\]

Мы уже выяснили, что \({p_1} = 2{p_0}\), поэтому:

\[m = \frac{{\left( {{p_1} — {p_0}} \right)S}}{g} = \frac{{\left( {2{p_0} — {p_0}} \right)S}}{g} = \frac{{{p_0}S}}{g}\]

Но если посмотреть на формулу (1), то видно, что \({p_0}S = P + {p_{атм}}S\), то есть в итоге окончательная формула будет выглядеть как:

\[m = \frac{{P + {p_{атм}}S}}{g}\]

Подставим численные значения величин в системе СИ и вычислим ответ:

\[m = \frac{{60 + {{10}^5} \cdot 20 \cdot {{10}^{ — 4}}}}{{10}} = 26\; кг \]