Условие задачи:
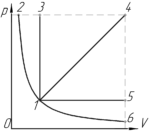В каком из изображенных на рисунке процессов, проведенных с постоянной массой идеального газа, температура газа достигает наибольшей величины? Кривая 2-1-6 описывается уравнением \(PV=const\). Рисунок, данный к задаче, приведен справа.
Задача №4.3.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
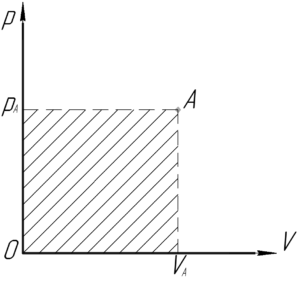Давайте подумаем, в каком точке PV-диаграммы достигается наибольшая температура. Для этого возьмем произвольную точку A на этой диаграмме (см. рисунок справа) и запишем уравнение Клапейрона-Менделеева:
\[{p_A}{V_A} = \frac{m}{M}R{T_A}\]
Выразим отсюда температуру \(T_A\):
\[{T_A} = \frac{{{p_A}{V_A}}}{{\frac{m}{M}R}} = \frac{{{p_A}{V_A}}}{{\nu R}}\]
В знаменателе этого выражения все величины постоянные. В числителе же мы видим произведение \({p_A}{V_A}\). Если мы взглянем на график, что это произведение олицетворяет не что иное, как площадь заштрихованного прямоугольника.
Получается, на PV-диаграмме максимальная температура достигается в точке, при которой будет наибольшая площадь прямоугольника, образованного осями координат и прямыми, параллельными этим же осям.
В нашей задаче точки 2, 3, 4 и точки 4, 5, 6 расположены на одной прямой. Значит наибольшая температура будет иметь место в точке 4, т.е. наибольшая температура достигается в процессе 1-4.
Ответ: 1-4.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.3.39 В трубке длиной 1,73 м, заполненной газом, находится столбик ртути
4.3.41 Горизонтально расположенный закрытый цилиндрический сосуд
4.3.42 На рисунке изображены гиперболы для трех идеальных газов с одинаковыми массами