Тонкостенный резиновый шар собственным весом 0,6 Н наполнен неоном и погружен в озеро

Условие задачи:

Тонкостенный резиновый шар собственным весом 0,6 Н наполнен неоном и погружен в озеро на глубину 120 м. Найти массу неона, если шар находится в положении равновесия. Температура воды 4° C. Натяжением резины пренебречь.

Задача №4.2.103 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(P=0,6\) Н, \(h=120\) м, \(t=4^\circ\) C, \(m-?\)

Решение задачи:

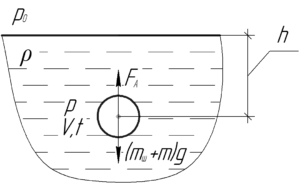На резиновый шар действуют такие силы: сила Архимеда \(F_А\) и суммарная сила тяжести \(\left( {{m_ш}g + mg} \right)\), действующая на шар с неоном. Так как шар находится в равновесии, то эти силы компенсируют друг друга, то есть справедливо равенство:

\[{F_А} = {m_ш}g + mg\;\;\;\;(1)\]

Собственный вес резинового шара \(P\) равен силе тяжести \({m_ш}g\), действующей на этот шар, поэтому:

\[P = {m_ш}g\;\;\;\;(2)\]

Выталкивающую силу воды \(F_А\) определяют по такой формуле:

\[{F_А} = \rho Vg\;\;\;\;(3)\]

Здесь \(\rho\) — плотность воды, равная 1000 кг/м³.

Чтобы определить объем шара \(V\) на глубине \(h\), запишем уравнение Клапейрона-Менделеева для неона:

\[pV = \frac{m}{M}RT\]

Молярная масса неона \(M\) равна 0,020 кг/моль. Выразим объем шара:

\[V = \frac{{mRT}}{{pM}}\]

Поскольку стенка шара является тонкой, то давление неона внутри резинового шара равно внешнему давлению воды. Последнее определяется по закону Паскаля:

\[p = {p_0} + \rho gh\]

В этой формуле \(p_0\) — атмосферное давление, равное 100 кПа.

\[V = \frac{{mRT}}{{\left( {{p_0} + \rho gh} \right)M}}\]

Формула (3) для определения выталкивающей силы станет такой:

\[{F_А} = \frac{{\rho mgRT}}{{\left( {{p_0} + \rho gh} \right)M}}\;\;\;\;(4)\]

Подставим выражения (2) и (4) в формулу (1), тогда:

\[\frac{{\rho mgRT}}{{\left( {{p_0} + \rho gh} \right)M}} = P + mg\]

Осталось только выразить из полученного равенства массу неона \(m\):

\[\frac{{\rho mgRT — \left( {{p_0} + \rho gh} \right)Mmg}}{{\left( {{p_0} + \rho gh} \right)M}} = P\]

\[\frac{{mg\left( {\rho RT — \left( {{p_0} + \rho gh} \right)M} \right)}}{{\left( {{p_0} + \rho gh} \right)M}} = P\]

\[m = \frac{{PM\left( {{p_0} + \rho gh} \right)}}{{\rho RT — \left( {{p_0} + \rho gh} \right)M}}\]

Переведём температуру в систему СИ:

\[4^\circ\;C  = 277\;К\]

Произведём вычисления:

\[m = \frac{{0,6 \cdot 0,02 \cdot \left( {100 \cdot {{10}^3} + 1000 \cdot 10 \cdot 120} \right)}}{{1000 \cdot 8,31 \cdot 277 — \left( {100 \cdot {{10}^3} + 1000 \cdot 10 \cdot 120} \right) \cdot 0,02}} = 6,85 \cdot {10^{ — 3}}\;кг = 685\;мг\]

Ответ: 685 мг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.102 В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами
4.2.104 Давление воздуха в сосуде равно 102,4 кПа. Вместимость цилиндра разрежающего насоса
4.2.105 Компрессор всасывает в 1 мин 3 м3 сухого воздуха при температуре 290 К и давлении 100 кПа