Состояние одного киломоля идеального газа менялось по графику 1-2-3. Определить

Условие задачи:

Состояние одного киломоля идеального газа менялось по графику 1-2-3. Определить конечный объем газа, если \(p_1=150\) кПа, \(T_1=300\) К, \(p_2=370\) кПа, \(T_2=450\) К.

Задача №4.2.96 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=1\) кмоль, \(p_1=150\) кПа, \(T_1=300\) К, \(p_2=370\) кПа, \(T_2=450\) К, \(V_3-?\)

Решение задачи:

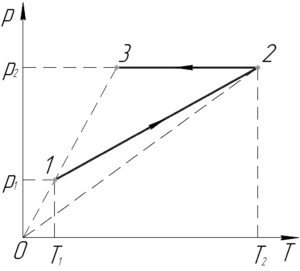Обратите внимание, что точки 1 и 3 лежат на одной прямой, проходящей через начало координат, при этом перед нами график зависимости давления газа от температуры (график p-T). Если бы через эти точки были соединены на графике, то на этом участке над газом производился бы изохорный процесс. Но так как они не соединены, мы можем только утверждать, что объемы газа в этих точках одинаковы, то есть \(V_1=V_3\).

Исходя из этого равенства, нам достаточно найти объем газа \(V_1\), который легко определить из уравнения Клапейрона-Менделеева, записанного для газа в состоянии 1.

\[{p_1}{V_1} = \nu R{T_1}\]

Здесь \(R\) – универсальная газовая постоянная, равная 8,31 Дж/(моль·К).

\[{V_1} = \frac{{\nu R{T_1}}}{{{p_1}}}\]

Ранее было доказано, что \(V_1=V_3\), поэтому:

\[{V_3} = \frac{{\nu R{T_1}}}{{{p_1}}}\]

Посчитаем ответ:

\[{V_3} = \frac{{{{10}^3} \cdot 8,31 \cdot 300}}{{150 \cdot {{10}^3}}} = 16,62\;м^3\]

Ответ: 16,62 м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.95 Объем пузырька, всплывающего на поверхность со дна озера, увеличился в два раза
4.2.97 Сосуд объемом 5 л разделен перегородкой на две части, заполненные одним газом
4.2.98 При некотором процессе идеального газа связь между давлением и объемом газа pV^3=const