Условие задачи:
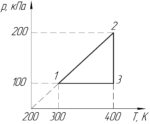 На PT-диаграмме изображен замкнутый процесс, который совершает кислород некоторой массы. Известно, что максимальный объем, который занимал газ в этом процессе, 16,4 дм3. Определите массу газа в точке 1. Значения \(T_1\), \(T_2\), \(p_1\), \(p_2\) указаны на рисунке.
На PT-диаграмме изображен замкнутый процесс, который совершает кислород некоторой массы. Известно, что максимальный объем, который занимал газ в этом процессе, 16,4 дм3. Определите массу газа в точке 1. Значения \(T_1\), \(T_2\), \(p_1\), \(p_2\) указаны на рисунке.
Задача №4.2.73 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(V_{max}=16,4\) дм3, \(p_1=p_3=100\) кПа, \(p_2=200\) кПа, \(T_1=300\) К, \(T_2=T_3=400\) К, \(m_1-?\)
Решение задачи:
 Во-первых, разберемся в какой точке графика процесса газ занимает наибольший объем. Для этого запишем уравнение Клапейрона-Менделеева:
Во-первых, разберемся в какой точке графика процесса газ занимает наибольший объем. Для этого запишем уравнение Клапейрона-Менделеева:
\[pV = \nu RT\]
Выразим из уравнения отношение \(\frac{p}{T}\), поскольку для любой прямой, проведённой через начало координат, оно равно тангенсу угла наклона прямой к положительному направлению оси T:
\[\frac{p}{T} = \frac{{\nu R}}{V}\]
\[tg\alpha = \frac{{\nu R}}{V}\]
Отсюда видно, что чем больше угол \(\alpha\), тем меньше объем газа \(V\), и наоборот.
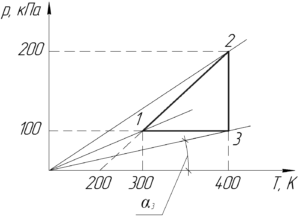
Обязательно покажем на графике начало координат (на схеме к условию оно не показано). Проведём прямые через начало координат и точки 1,2 и 3. Угол \(\alpha_3\) наименьший, поэтому газ занимает наибольший объем в точке 3, то есть:
\[{V_3} = {V_{max}}\;\;\;\;(1)\]
Запишем уравнение Клапейрона-Менделеева для газа в точке 1:
\[{p_1}{V_1} = \frac{m_1}{M}R{T_1}\]
Здесь \(M\) — молярная масса кислорода, равная 0,032 кг/моль. Выразим массу газа \(m_1\):
\[{m_1} = \frac{{{p_1}{V_1}M}}{{R{T_1}}}\;\;\;\;(2)\]
Чтобы определить объем \(V_1\) заметим, что процесс 3-1 является изобарным, поэтому можно применить закон Гей-Люссака:
\[\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_3}}}{{{T_3}}}\]
\[{V_1} = {V_3}\frac{{{T_1}}}{{{T_3}}}\]
Полученное выражение подставим в формулу (2), тогда:
\[{m_1} = \frac{{{p_1}{V_3}M}}{{R{T_1}}}\frac{{{T_1}}}{{{T_3}}} = \frac{{{p_1}{V_3}M}}{{R{T_3}}}\]
Учитывая (1), получим следующую конечную формулу:
\[{m_1} = \frac{{{p_1}{V_{max}}M}}{{R{T_3}}}\]
Переведем объем \(V_{max}\) в систему СИ:
\[16,4\;дм^3 = 16,4 \cdot {10^{ — 3}}\;м^3\]
Численно масса газа в точке 1 \(m_1\) равна:
\[{m_1} = \frac{{100 \cdot {{10}^3} \cdot 16,4 \cdot {{10}^{ — 3}} \cdot 0,032}}{{8,31 \cdot 400}} = 0,016\;кг\]
Ответ: 0,016 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.72 На рисунке показан график процесса, происходящего с идеальным газом. Укажите точки
4.2.74 Если нагреть 1 моль идеального газа на 1 К при постоянном объеме, то давление возрастет
4.2.75 Имеется два сосуда с одним и тем же газом при одинаковой температуре. Плотность газа
Почему мы можем использовать закон Гей-Люссака??? В закон сказано, что V/T=const, если молярная масса- const и давление — const
Почему нет? Процесс 3-1 явно изобарный.
С чего вы взяли, что масса константа?
Да, строго говоря об этом не сказано в условии, но у меня есть большие сомнения, что задача будет решаемой, есть масса непостоянна.
Это существенное условие, которое так или иначе должно быть отражено в условии, тем более в задаче на термодинамический цикл.