На дне цилиндра, наполненного воздухом, плотность которого 1,29 кг/м3, лежит полый

Условие задачи:

На дне цилиндра, наполненного воздухом, плотность которого 1,29 кг/м³, лежит полый металлический шарик радиусом 1 см. До какого давления нужно сжать воздух в цилиндре, чтобы шарик всплыл? Опыт проводят при температуре 290 К, масса шарика 5 г.

Задача №4.2.85 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_0=1,29\) кг/м³, \(r=1\) см, \(T=290\) К, \(m_ш=5\) г, \(p-?\)

Решение задачи:

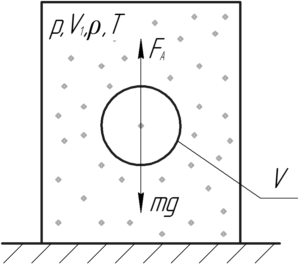Шарик всплывёт, если сила Архимеда \(F_А\) станет равной силе тяжести \({m_ш}g\):

\[{F_А} = {m_ш}g\;\;\;\;(1)\]

При этом силу Архимеда определяют по формуле:

\[{F_А} = \rho Vg\;\;\;\;(2)\]

Тогда равенство (1) примет вид:

\[\rho Vg = {m_ш}g\]

\[\rho V = {m_ш}\;\;\;\;(3)\]

Когда это произойдёт? При увеличении давления в цилиндре повысится плотность воздуха, а значит увеличится и выталкивающая сила \(F_А\) (смотрите формулу (2)). Когда выполнится условие (1), изначально лежащий на дне цилиндра шарик всплывёт.

Объем шарика \(V\) определяют по формуле:

\[V = \frac{4}{3}\pi {r^3}\;\;\;\;(4)\]

Плотность воздуха \(\rho\) равна отношению массы воздуха в цилиндре \(m\) к объему цилиндра \(V_1\). Запишем уравнение Клапейрона-Менделеева и поделим обе части уравнения на объем \(V_1\), тогда:

\[p{V_1} = \frac{m}{M}RT\]

\[p = \frac{m}{{M{V_1}}}RT\]

\[p = \frac{\rho }{M}RT\]

Откуда плотность воздуха \(\rho\) равна:

\[\rho  = \frac{{pM}}{{RT}}\;\;\;\;(5)\]

С учётом выражений (4) и (5) равенство (3) примет вид:

\[\frac{{pM}}{{RT}} \cdot \frac{4}{3}\pi {r^3} = {m_ш}\]

В итоге получим:

\[p = \frac{{3{m_ш}RT}}{{4\pi {r^3}M}}\]

Здесь \(M\) – молярная масса воздуха, равная 0,029 кг/моль. Переведём радиус шарика и его массу в систему СИ:

\[1\;см = 0,01\;м\]

\[5\;г = 0,005\;кг\]

Произведём вычисления:

\[p = \frac{{3 \cdot 0,005 \cdot 8,31 \cdot 290}}{{4 \cdot 3,14 \cdot {{0,01}^3} \cdot 0,029}} = {10^8}\;Па = 0,1\;ГПа\]

Ответ: 0,1 ГПа.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.84 Внутри замкнутого цилиндра, наполненного воздухом, находится шарик радиусом 3 см
4.2.86 В замкнутом сосуде к верхней стенке на пружине жесткостью 4 Н/м подвешена сфера
4.2.87 Во сколько раз изменится температура идеального газа, если уменьшить его объем