Какой радиус должен иметь наполненный гелием воздушный шар, чтобы он мог подняться

Условие задачи:

Какой радиус должен иметь наполненный гелием воздушный шар, чтобы он мог подняться в воздух, если масса 1 м² оболочки шара 50 г? Температура воздуха 27° C, давление 100 кПа.

Задача №4.2.80 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m_0=50\) г/м², \(t=27^\circ\) C, \(p_0=100\) кПа, \(r-?\)

Решение задачи:

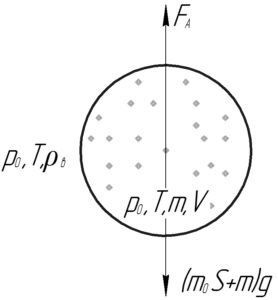Шар поднимется в воздух, если сила Архимеда станет равной силе тяжести, то есть выполнится условие плавания тел:

\[{F_А} = \left( {{m_0}S + m} \right)g\]

В этой формуле \(S\) – площадь поверхности воздушного шара, \(m\) – масса гелия, заключённого в шаре.

Выталкивающую силу (силу Архимеда) найдём по следующей формуле:

\[{F_А} = {\rho _в}gV\]

Здесь \(\rho_в\) – плотность окружающего воздуха, а \(V\) – объем воздушного шара. Тогда:

\[{\rho _в}gV = \left( {{m_0}S + m} \right)g\]

\[{\rho _в}V = {m_0}S + m\;\;\;\;(1)\]

Чтобы определить плотность воздуха \(\rho_в\) и массу гелия \(m\), запишем дважды уравнение Клапейрона-Менделеева для воздуха произвольного объема \(V_1\) и гелия. Отметим, что давления окружающего воздуха и гелия внутри шара равны друг другу:

\[\left\{ \begin{gathered}
{p_0}{V_1} = \frac{{{m_1}}}{{{M_в}}}RT \hfill \\
{p_0}V = \frac{m}{M}RT \hfill \\
\end{gathered} \right.\]

Молярная масса воздуха \(M_в\) равна 0,029 кг/моль, гелия \(M\) – 0,004 кг/моль.

Поделим обе части верхнего уравнения системы на \(V_1\). Отношение массы воздуха \(m_1\) к объему \(V_1\), который занимает эта масса воздуха, есть плотность воздуха \(\rho_в\), поэтому:

\[\left\{ \begin{gathered}
{p_0} = \frac{{{\rho _1}}}{{{M_в}}}RT \hfill \\
{p_0}V = \frac{m}{M}RT \hfill \\
\end{gathered} \right.\]

Из первого уравнения выразим плотность воздуха \(\rho_в\), а из второго – массу гелия \(m\):

\[\left\{ \begin{gathered}
{\rho _в} = \frac{{{p_0}{M_в}}}{{RT}} \hfill \\
m = \frac{{{p_0}VM}}{{RT}} \hfill \\
\end{gathered} \right.\]

С учётом полученных выражений формула (1) примет вид:

\[\frac{{{p_0}{M_в}}}{{RT}}V = {m_0}S + \frac{{{p_0}VM}}{{RT}}\]

Площадь поверхности шара \(S\) и объем шара \(V\) определяют по формулам:

\[\left\{ \begin{gathered}
S = 4\pi {r^2} \hfill \\
V = \frac{4}{3}\pi {r^3} \hfill \\
\end{gathered} \right.\]

Тогда:

\[\frac{{{p_0}{M_в}}}{{RT}} \cdot \frac{4}{3}\pi {r^3} = {m_0} \cdot 4\pi {r^2} + \frac{{{p_0}M}}{{RT}} \cdot \frac{4}{3}\pi {r^3}\]

\[\frac{{{p_0}{M_в}}}{{RT}} \cdot \frac{r}{3} = {m_0} + \frac{{{p_0}M}}{{RT}} \cdot \frac{r}{3}\]

\[\frac{{r{p_0}\left( {{M_в} – M} \right)}}{{3RT}} = {m_0}\]

Решение задачи в общем виде получилось таким:

\[r = \frac{{3{m_0}RT}}{{{p_0}\left( {{M_в} – M} \right)}}\]

Переведём некоторые величины в систему СИ:

\[50\;г/м^2 = 0,05\;кг/м^2\]

\[27^\circ\;C  = 300\;К\]

Посчитаем численное значение радиуса шара \(r\):

\[r = \frac{{3 \cdot 0,05 \cdot 8,31 \cdot 300}}{{100 \cdot {{10}^3} \cdot \left( {0,029 – 0,004} \right)}} = 0,15\;м\]

Ответ: 0,15 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.79 В некотором процессе давление и объем идеального газа связаны соотношением
4.2.81 Надувной шарик, заполненный гелием, удерживают на нити. Найдите натяжение нити
4.2.82 Два баллона с объемами 20 и 10 л соединены длинной тонкой трубкой и содержат 6 моль