Условие задачи:
Два сосуда, содержащих одинаковую массу одного и того же газа, соединены трубкой с краном. В первом давлении 100 кПа, во втором – 300 кПа. Температура одинакова. Какое давление установится после открытия крана?
Задача №4.2.68 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m\), \(p_1=100\) кПа, \(p_2=300\) кПа, \(T\), \(p-?\)
Решение задачи:
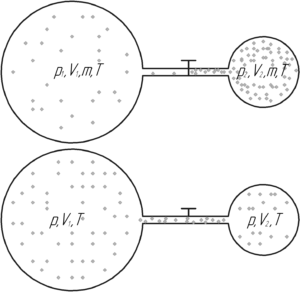Запишем три раза уравнение Клапейрона-Менделеева: для газов в сосудах до открытия крана и после:
\[\left\{ \begin{gathered}
{p_1}{V_1} = \frac{m}{M}RT \;\;\;\;(1)\hfill \\
{p_2}{V_2} = \frac{m}{M}RT \;\;\;\;(2)\hfill \\
p\left( {{V_1} + {V_2}} \right) = \frac{{2m}}{M}RT \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Из уравнений (1) и (2) следует, что:
\[{p_1}{V_1} = {p_2}{V_2}\]
\[\frac{{{V_1}}}{{{V_2}}} = \frac{{{p_2}}}{{{p_1}}}\;\;\;\;(4)\]
Также сложим уравнения (1) и (2), тогда получим:
\[{p_1}{V_1} + {p_2}{V_2} = \frac{{2m}}{M}RT\]
Так как равны правые части получившегося равенства и уравнения (3), то равны и левые, то есть:
\[p\left( {{V_1} + {V_2}} \right) = {p_1}{V_1} + {p_2}{V_2}\]
Выразим давление \(p\):
\[p = \frac{{{p_1}{V_1} + {p_2}{V_2}}}{{{V_1} + {V_2}}}\]
Поделим числитель и знаменатель дроби справа на \(V_2\), тогда:
\[p = \frac{{{p_1}\frac{{{V_1}}}{{{V_2}}} + {p_2}}}{{\frac{{{V_1}}}{{{V_2}}} + 1}}\]
Учитывая (4), получим:
\[p = \frac{{{p_1} \cdot \frac{{{p_2}}}{{{p_1}}} + {p_2}}}{{\frac{{{p_2}}}{{{p_1}}} + 1}}\]
\[p = \frac{{2{p_1}{p_2}}}{{{p_1} + {p_2}}}\]
Задача решена в общем виде, давайте посчитаем ответ:
\[p = \frac{{2 \cdot 100 \cdot {{10}^3} \cdot 300 \cdot {{10}^3}}}{{100 \cdot {{10}^3} + 300 \cdot {{10}^3}}} = 150000\;Па = 150\;кПа\]
Ответ: 150 кПа.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.67 В откачанной ампуле объемом 3 см3 содержится радий массой 5 г в течение одного года
4.2.69 Сколько молей газа следует добавить к одному молю данного газа, чтобы его давление
4.2.70 В открытом цилиндре находится 90 г газа. Температуру газа увеличили от 300 до 450 К