Условие задачи:
Чему равно среднее расстояние между молекулами насыщенного водяного пара при температуре 100° C?
Задача №4.1.65 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=100^\circ\) C, \(l-?\)
Решение задачи:
 Рассмотрим водяной пар в некотором произвольном количестве, равном \(\nu\) моль. Чтобы определить объем \(V\), занимаемый данным количеством водяного пара, нужно воспользоваться уравнением Клапейрона-Менделеева:
Рассмотрим водяной пар в некотором произвольном количестве, равном \(\nu\) моль. Чтобы определить объем \(V\), занимаемый данным количеством водяного пара, нужно воспользоваться уравнением Клапейрона-Менделеева:
\[pV = \nu RT\]
\[V = \frac{{\nu RT}}{p}\]
В этой формуле \(R\) — универсальная газовая постоянная, равная 8,31 Дж/(моль·К). Давление насыщенного водяного пара \(p\) при температуре 100° C равно 100 кПа, это известный факт, и его должен знать каждый учащийся.
Чтобы определить количество молекул водяного пара \(N\), воспользуемся следующей формулой:
\[N = \nu {N_А}\]
Здесь \(N_А\) — число Авогадро, равное 6,023·1023 1/моль.
Тогда на каждую молекулу приходится куб объема \(V_0\), очевидно определяемый по формуле:
\[{V_0} = \frac{V}{N}\]
\[{V_0} = \frac{{\nu RT}}{{p\nu {N_А}}} = \frac{{RT}}{{p{N_А}}}\]
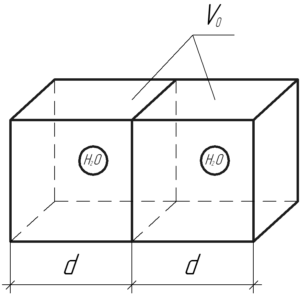
Теперь посмотрите на схему к задаче. Каждая молекула условно находится в своем кубе, расстояние между двумя молекулами может меняться от 0 до \(2d\), где \(d\) — длина ребра куба. Среднее же расстояние \(l\) будет равно длине ребра куба \(d\):
\[l = d\]
Длину ребра \(d\) можно найти так:
\[d = \sqrt[3]{{{V_0}}}\]
В итоге получим такую формулу:
\[l = \sqrt[3]{{\frac{{RT}}{{p{N_А}}}}}\]
Переведем температуру в шкалу Кельвина и посчитаем ответ:
\[100^\circ\;C = 373\;К\]
\[l = \sqrt[3]{{\frac{{8,31 \cdot 373}}{{100 \cdot {{10}^3} \cdot 6,023 \cdot {{10}^{23}}}}}} = 3,72 \cdot {10^{ — 9}}\;м = 3,72\;нм\]
Ответ: 3,72 нм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.1.64 Какое количество вещества содержится в алюминиевой ложке массы 27 г? Относительная
4.1.66 Молекула двухатомного газа содержит 16 протонов и 16 нейтронов. Чем равна плотность
4.1.67 В сосуде вместимостью 4 м3 находится 4,8 кг идеального газа. Средняя квадратичная
На самом деле максимально возможное расстояние между молекулами — диагональ прямоугольного параллелепипеда сторонами d*2d*d — d*sqrt(6). Поэтому среднее расстояние — sqrt(1.5) (если точно, то sqrt(1.466) — с учётом вероятности попадания в каждую точку куба)
Вы слишком доверились моему чертежу. Нарисуйте 9 таких кубиков и оцените в таком случае среднее расстояние.
Как Вы перешли от максимального к среднему — я не понимаю, как оценили вероятность попадания в каждую точку куба — тоже (вроде как всё равновероятно, не?).
Вы правы. В этом случае лучше будет рассматривать шар диаметром d, и искать среднее расстояние в нём. Вероятность попадания молекулы в угол куба крайне мала.
А если одна из молекул находится в правом верхнем углу кубика, а другая в левом нижнем углу другого кубика? Ведь в этом случае расстояние между ними (молекулами) не равно 2d?
Верно, но в задаче спрашивают про среднее расстояние.
Расстояние будет колебаться от 0 до 2d, т.е. в среднем будет равно d.
А что такое среднее? Среднее арифметическое? Если так, то надо просуммировать все расстояния между всеми парами молекул и разделить на количество слагаемых. Тогда это решение неверное.
И почему у Вас молекулы внутри кубика колеблются не по всему объему?
Да, среднее арифметическое.
Да, можно суммировать, и вы получите такое же среднее расстояние d, поскольку молекулы распределены равномерно (всё-таки мы подразумеваем, что флуктуаций молекул в выбранном объеме V нет). То есть если сделать «снимок», то на каждую молекулу придется объем V0, равный V/N.
«расстояние между двумя молекулами может меняться от 0 до 2d»
Почему вы так думаете ?
Посмотрите на схему. Каждая молекула условно находится в своём кубе.
Тогда максимальное расстояние между молекулами будет иметь место, когда молекулы «прижаты» к крайним граням изображенных двух кубов. Оно будет равно 2d. А минимальное — когда молекулы будут находиться у общей грани этих двух кубов. Оно уже равно 0.
Спасибо