Заряженная частица движется в магнитном поле по окружности радиусом 4 см

Условие задачи:

Заряженная частица движется в магнитном поле по окружности радиусом 4 см. Скорость частицы 1000 км/с, индукция магнитного поля 0,3 Тл. Найти заряд частицы, если её энергия равна 1,92·10^-15 Дж.

Задача №8.2.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=4\) см, \(\upsilon=1000\) км/с, \(B=0,3\) Тл, \(W=1,92 \cdot 10^{-15}\) Дж, \(q-?\)

Решение задачи:

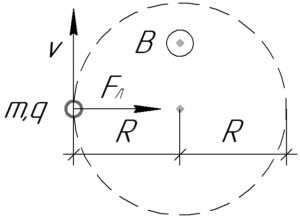На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:

\[{F_Л} = B\upsilon q\sin \alpha \;\;\;\;(1)\]

Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость частицы, \(q\) — модуль заряда частицы, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции (так как иного не сказано в условии, то \(\alpha=90^\circ\)).

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца.

Так как в условии не сказано какого знака заряд частицы, то условно примем его положительным. Значит в нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.

Сила Лоренца \(F_Л\) сообщает частице центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:

\[{F_Л} = m{a_ц}\;\;\;\;(2)\]

Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]

Подставим (3) в (2), тогда:

\[{F_Л} = \frac{{m{\upsilon ^2}}}{R}\;\;\;\;(4)\]

Приравняем правые части (1) и (4):

\[B\upsilon q\sin \alpha = \frac{{m{\upsilon ^2}}}{R}\]

Имеем:

\[Bq\sin \alpha = \frac{{m\upsilon }}{R}\]

\[q = \frac{{m\upsilon }}{{BR\sin \alpha }}\;\;\;\;(5)\]

Кинетическая энергия частицы \(W\) равна:

\[W = \frac{{m{\upsilon ^2}}}{2}\]

Выразим из этой формулы неизвестную массу частицы \(m\):

\[m = \frac{{2W}}{{{\upsilon ^2}}}\;\;\;\;(6)\]

Осталось только подставить выражение (6) в формулу (5):

\[q = \frac{\upsilon }{{BR\sin \alpha }} \cdot \frac{{2W}}{{{\upsilon ^2}}}\]

\[q = \frac{{2W}}{{B\upsilon R\sin \alpha }}\]

Численный ответ равен:

\[q = \frac{{2 \cdot 1,92 \cdot {{10}^{ — 15}}}}{{0,3 \cdot 1000 \cdot {{10}^3} \cdot 0,04 \cdot \sin 90^\circ }} = 3,2 \cdot {10^{ — 19}}\;Кл\]

Интересно, что заряд частицы равен по модулю двум зарядам электрона \(2e\).

Ответ: 2e.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.9 Протон описал окружность радиусом 5 см в однородном магнитном поле с индукцией 20 мТл
8.2.11 Электрон движется в однородном магнитном поле с индукцией 0,1 Тл по окружности
8.2.12 Протон движется в однородном магнитном поле с индукцией 1 Тл со скоростью 200000 км/с