Условие задачи:
В однородном магнитном поле с индукцией 4,9 Тл горизонтально подвешен на двух нитях прямолинейный проводник массой 0,6 кг и длиной 0,3 м, по которому течет ток силой в 2 А. На какой угол от вертикали отклонятся нити, если линии индукции магнитного поля направлены вертикально вниз?
Задача №8.1.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(B=4,9\) Тл, \(m=0,6\) кг, \(l=0,3\) м, \(I=2\) А, \(\beta-?\)
Решение задачи:
 На проводник с током, находящийся в магнитном поле, действует сила Ампера \(F_А\). Направление действия силы Ампера определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по току в проводнике, то большой палец, оставленный на 90°, покажет направление силы Ампера.
На проводник с током, находящийся в магнитном поле, действует сила Ампера \(F_А\). Направление действия силы Ампера определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по току в проводнике, то большой палец, оставленный на 90°, покажет направление силы Ампера.
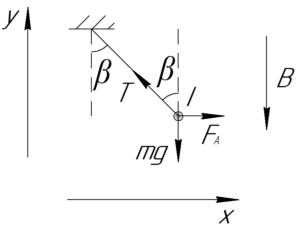
В нашем случае вектор магнитной индукции \(B\) направлен вертикально вниз. Чтобы проводник отклонялся на нитях вправо (то есть сила Ампера была направлена вправо), ток должен идти перпендикулярно экрану по направлению к нам.
Понятно, что проводник находится в равновесии под действием трёх сил: силы тяжести \(mg\), силы натяжения нитей \(T\) и силы Ампера \(F_А\). Запишем первый закон Ньютона в проекции на оси \(x\) и \(y\):
\[\left\{ \begin{gathered}
ox:T \cdot \cos \beta = mg \hfill \\
oy:T \cdot \sin \beta = {F_А} \hfill \\
\end{gathered} \right.\]
Ускорение свободного падения \(g\) равно 10 м/с2.
Чтобы избавиться от неизвестной силы натяжения нитей \(T\), поделим нижнее равенство на верхнее, тогда получим:
\[tg\beta = \frac{{{F_А}}}{{mg}}\;\;\;\;(1)\]
Величину силы Ампера \(F_А\) можно определить по следующей формуле:
\[{F_А} = IBl\sin \alpha \;\;\;\;(2)\]
Здесь \(\alpha\) — угол между проводником и вектором магнитной индукции, который для этой задачи равен 90° согласно условию (магнитное поле — вертикальное, а проводник подвешен горизонтально). Подставим в формулу (1) выражение (2):
\[tg\beta = \frac{{IBl\sin \alpha }}{{mg}}\]
Откуда искомый угол \(\beta\) равен:
\[\beta = arctg\left( {\frac{{IBl\sin \alpha }}{{mg}}} \right)\]
Отлично, задача решена. Подставим теперь данные из условия задачи в полученную формулу и посчитаем численный ответ:
\[\beta = arctg\left( {\frac{{2 \cdot 4,9 \cdot 0,3 \cdot \sin 90^\circ }}{{0,6 \cdot 10}}} \right) = 26,1^\circ \]
Ответ: 26,1°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.1.13 На прямолинейный проводник длиной 40 см и током 20 А, расположенный под углом
8.1.15 Прямой провод, по которому течет постоянный ток, расположен в однородном магнитном
8.1.16 По проводнику АБ протекает постоянный ток. Проводник помещен в однородное магнитное
У вас ошибка в решении, проекция mg на Ох будет ровна нулю и будет синус угла, а сила ампера не равна нулю!
Почему на рисунке сила натяжения нити одна?
У нас в решении сила натяжении одна, равная сумме двух