Условие задачи:

Прямой проводник с током 1 А приобрел под действием перпендикулярного ему магнитного поля ускорение 2 м/с². Площадь поперечного сечения проводника 1 мм², плотность его материала 2500 кг/м³. Найти индукцию поля. Силу тяжести не учитывать.

Задача №8.1.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(I=1\) А, \(\alpha=90^\circ\), \(a=2\) м/с², \(S=1\) мм², \(\rho=2500\) кг/м³, \(B-?\)

Решение задачи:

На проводник, по которому течет ток, в магнитном поле действует сила Ампера. Величину этой силы можно определить по следующей формуле:

\[{F_А} = IBl\sin \alpha \;\;\;\;(1)\]

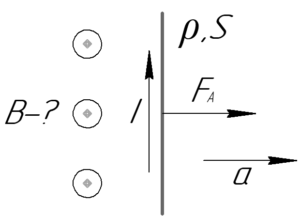
Направление действия силы Ампера определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по току в проводнике, то большой палец, оставленный на 90°, покажет направление силы Ампера. Если принять, что вектор магнитной индукции направлен к нам, а сила тока — вверх, то сила Ампера \(F_А\) будет направлена вправо.

Сила Ампера \(F_А\) ускоряет проводник. Из второго закона Ньютона следует, что:

\[{F_А} = ma\]

Учитывая формулу (1), имеем:

\[IBl\sin \alpha = ma\]

Очевидно, что массу проводника \(m\) можно определить как произведение плотности материала проводника \(\rho\) на его объем \(V\):

\[m = \rho V\]

Зная площадь сечения проводника \(S\), объем \(V\) можно найти по формуле:

\[V = Sl\]

Тогда имеем:

\[IBl\sin \alpha = \rho Sla\]

\[IB\sin \alpha = \rho Sa\]

Значит индукция магнитного поля \(B\) равна:

\[B = \frac{{\rho Sa}}{{I\sin \alpha }}\]

Численный ответ этой задачи равен:

\[B = \frac{{2500 \cdot {{10}^{ — 6}} \cdot 2}}{{1 \cdot \sin 90^\circ }} = 0,005\;Тл = 5\;мТл\]

Ответ: 5 мТл.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.1.11 Проводник массой 5 г на метр длины, по которому течет ток силой в 10 А, расположенный
8.1.13 На прямолинейный проводник длиной 40 см и током 20 А, расположенный под углом
8.1.14 В однородном магнитном поле с индукцией 4,9 Тл горизонтально подвешен на двух нитях