Решение: Определить силу тока, протекающего по плоскому контуру площадью 5 см2, находящемуся

Условие задачи:

Определить силу тока, протекающего по плоскому контуру площадью 5 см², находящемуся в однородном магнитном поле с индукцией 0,5 Тл, если максимальный механический момент, действующий со стороны поля, равен 0,25 мН·м.

Задача №8.3.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$S=5$ см², $B=0,5$ Тл, $M_{\max}=0,25$ мН·м, $I-?$

Решение задачи:

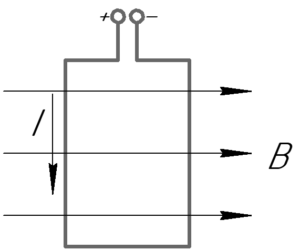Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил $M$ , который можно найти по следующей формуле:

$M = BIS\sin \alpha$

В этой формуле $B$ — индукция магнитного поля, $I$ — сила текущего в рамке (контуре) тока, $S$ — площадь рамки (контура), $\alpha$ — угол между нормалью к плоскости контура и вектором магнитной индукции.

Очевидно, что максимальный магнитный момент будет наблюдаться тогда, когда угол $\alpha$ между нормалью к плоскости контура и вектором магнитной индукции будет равен 90°, то есть плоскость контура будет параллельна линиям магнитной индукции (смотрите рисунок к задаче). Поэтому:

${M_{\max }} = BIS$

Откуда искомая сила $I$ равна:

$I = \frac{{{M_{\max }}}}{{BS}}$

Задача решена в общем, подставим данные задачи в формулу, переведя их в систему СИ, и посчитаем ответ:

$I = \frac{{0,25 \cdot {{10}^{ — 3}}}}{{0,5 \cdot 5 \cdot {{10}^{ — 4}}}} = 1\;А$