Условие задачи:
Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся в однородном магнитном поле с частотой 10 об/с, если амплитуда индуцируемой в рамке ЭДС 3 В.
Задача №8.4.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=10\) об/с, \(\rm E_{imax}=3\) В, \(\Phi_{max}-?\)
Решение задачи:
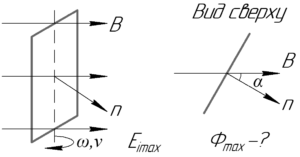 Если рамка вращается в поле с некоторой угловой скоростью \(\omega\), то магнитный поток через рамку \(\Phi\) изменяется по следующей формуле:
Если рамка вращается в поле с некоторой угловой скоростью \(\omega\), то магнитный поток через рамку \(\Phi\) изменяется по следующей формуле:
\[\Phi = {\Phi _{max }}\cos \omega t\]
Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока (то есть первой производной функции изменения потока от времени):
\[{\rm E_i} = — \Phi ^\prime \left( t \right)\]
Тогда:
\[{{\rm E}_i} = — {\left( {{\Phi _{max }}\cos \omega t} \right)^\prime }\]
\[{{\rm E}_i} = {\Phi _{max }}\omega \sin \omega t\]
Очевидно, что ЭДС индукции достигнет своего максимального значения, когда синус будет равен единице, поэтому:
\[{{\rm E}_{imax }} = {\Phi _{max }}\omega \]
Угловая скорость вращения \(\omega\) связана с частотой вращения \(\nu\) по такой формуле:
\[\omega = 2\pi \nu \]
Тогда:
\[{{\rm E}_{imax }} = 2\pi \nu {\Phi _{max }}\]
Откуда получим такую формулу:
\[{\Phi _{max }} = \frac{{{{\rm E}_{imax }}}}{{2\pi \nu }}\]
Посчитаем численный ответ:
\[{\Phi _{max }} = \frac{3}{{2 \cdot 3,14 \cdot 10}} = 0,048\;Вб\]
Ответ: 0,048 Вб.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.50 В магнитном поле с индукцией 0,01 Тл вращается стержень длиной 0,2 м с постоянной
8.4.52 При равномерном изменении силы тока через катушку из 500 витков в ней возникает
8.4.53 Соленоид, содержащий 1000 витков медной проволоки сечением 0,2 мм2, находится