Решение: Из проволоки длиной 20 см сделали квадратный контур. Найти максимальный вращающий

Условие задачи:

Из проволоки длиной 20 см сделали квадратный контур. Найти максимальный вращающий момент сил, действующий на контур, помещенный в магнитное поле с индукцией 0,1 Тл. По контуру течет ток 2 А.

Задача №8.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=20\) см, \(B=0,1\) Тл, \(I=2\) А, \(M_{\max}-?\)

Решение задачи:

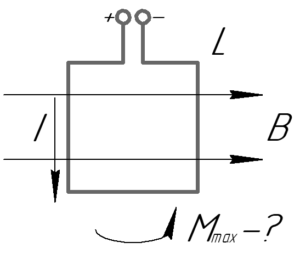Если в однородное магнитное поле внести рамку (или плоский контур, что то же самое), по которой течет ток, то в общем случае на стороны рамки будут действовать силы Ампера. Эти силы создадут вращающий момент сил \(M\), который можно найти по следующей формуле:

\[M = BIS\sin \alpha \]

В этой формуле \(B\) — индукция магнитного поля, \(I\) — сила текущего в рамке (контуре) тока, \(S\) — площадь рамки (контура), \(\alpha\) — угол между нормалью к плоскости контура и вектором магнитной индукции.

Очевидно, что максимальный магнитный момент будет наблюдаться тогда, когда угол \(\alpha\) между нормалью к плоскости контура и вектором магнитной индукции будет равен 90°, то есть плоскость контура будет параллельна линиям магнитной индукции (смотрите рисунок к задаче). Поэтому:

\[{M_{\max }} = BIS\;\;\;\;(1)\]

Понятно, что если из проволоки длиной \(L\) сделать квадратный контур, то длина стороны этого контура \(a\) будет равна:

\[a = \frac{L}{4}\]

В таком случае, площадь квадратного контура \(S\) будет равна:

\[S = {a^2}\]

\[S = \frac{{{L^2}}}{{16}}\]

Учитывая это, формула (1) примет вид:

\[{M_{\max }} = \frac{{BI{L^2}}}{{16}}\]

Посчитаем теперь численный ответ к задаче:

\[{M_{\max }} = \frac{{0,1 \cdot 2 \cdot {{0,2}^2}}}{{16}} = 5 \cdot {10^{ — 4}}\;Н \cdot м\]