Условие задачи:
Два металлических стержня расположены вертикально и замкнуты вверху проводником. По ним без трения и нарушения контакта скользит перемычка длиной 2 см и массой 1 г. Вся система находится в однородном магнитном поле с индукцией 0,01 Тл, перпендикулярной к плоскости рамки. Установившаяся скорость 0,8 м/с. Найти сопротивление перемычки. Сопротивлением стержней и провода пренебречь.
Задача №8.4.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=2\) см, \(m=1\) г, \(B=0,01\) Тл, \(\upsilon=0,8\) м/с, \(R-?\)
Решение задачи:
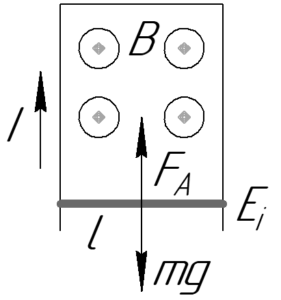 Условно примем магнитное поле, направленное к нам (смотрите рисунок к решению задачи).
Условно примем магнитное поле, направленное к нам (смотрите рисунок к решению задачи).
Итак, вполне понятно, что перемычка в начале будет скользить вниз под действием силы тяжести. Поскольку скользящая перемычка находится в горизонтальном магнитном поле, значит в ней будет возникать ЭДС индукции \(\rm E_i\), равная:
\[{{\rm E}_i} = B\upsilon l\]
Из-за возникающей ЭДС индукции \(\rm E_i\) в цепи, состоящей из стержней, проводника и перемычки, будет течь ток, который можно определить, используя закон Ома. Направление тока — по часовой стрелке (смотрите рисунок к решению) — чтобы это доказать, нужно выделить в перемычке положительный заряд и узнать направление действующей на него силы Лоренца. Направление тока совпадает с направлением силы Лоренца, действующей на положительный заряд.
\[I = \frac{{{{\rm E}_i}}}{R}\]
То есть имеем:
\[I = \frac{{B\upsilon l}}{R}\;\;\;\;(1)\]
Из-за того, что в перемычке потечет ток, на неё станет действовать сила Ампера \(F_А\), причем она будет направлена вертикально вверх согласно правилу левой руки. Её значение можно найти по формуле:
\[{F_А} = IBl\]
Учитывая (1), имеем:
\[{F_А} = \frac{{{B^2}\upsilon {l^2}}}{R}\;\;\;\;(2)\]
Интересно, что начальное ускоренное движение перемычки под действием силы тяжести \(mg\) быстро сменится на равномерное из-за дополнительного действия силы Ампера \(F_А\), поскольку чем быстрее движется перемычка (т.е. чем больше ЭДС индукции), тем выше индукционный ток в цепи, и тем выше сила Ампера \(F_А\), тормозящая движение перемычки. Для равномерного движения перемычки применим первый закон Ньютона:
\[{F_А} = mg\]
Принимая во внимание (2), получим:
\[\frac{{{B^2}\upsilon {l^2}}}{R} = mg\]
Откуда сопротивление перемычки \(R\) равно:
\[R = \frac{{{B^2}\upsilon {l^2}}}{{mg}}\]
Посчитаем численный ответ задачи:
\[R = \frac{{{{0,01}^2} \cdot 0,8 \cdot {{0,02}^2}}}{{0,001 \cdot 10}} = 3,2 \cdot {10^{ — 6}}\;Ом = 3,2\;мкОм\]
Ответ: 3,2 мкОм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.54 Какой ток идет через гальванометр с сопротивлением 100 Ом, присоединенный
8.4.56 Две параллельные вертикальные медные шины, находящиеся в 1 м друг от друга
8.4.57 В однородном магнитном поле с индукцией 10 мТл расположены вертикально