Условие задачи:
Вычислить тормозной путь автомобиля, имеющего начальную скорость 60 км/ч, на мокрой дороге, если он тормозит с ускорением 3 м/с2.
Задача №1.3.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=60\) км/ч, \(a=3\) м/с2, \(S-?\)
Решение задачи:
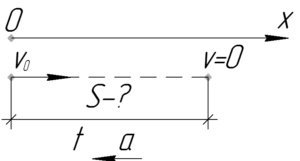 Понятно, что скорость автомобиля в конце тормозного пути равна нулю.
Понятно, что скорость автомобиля в конце тормозного пути равна нулю.
\[\upsilon = 0\]
Применим следующую формулу.
\[{\upsilon ^2} — \upsilon _0^2 = — 2aS\]
«Минус» в правой части говорит о том, что скорость автомобиля уменьшается. Учитывая все сказанное, в итоге имеем такое выражение:
\[ — \upsilon _0^2 = — 2aS\]
\[\upsilon _0^2 = 2aS\]
Осталось только выразить искомый тормозной путь \(S\), подставить численные данные и сосчитать ответ.
\[S = \frac{{\upsilon _0^2}}{{2a}}\]
Заметим, что начальная скорость \(\upsilon\) дана в км/ч. Перед тем, как подставлять значение \(\upsilon_0\) в формулу, необходимо перевести ее в систему СИ, то есть в м/с.
Чтобы перевести скорость из км/ч в м/с необходимо произвести следующие действия.
\[60\; км/ч = \frac{{60 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{600}}{{36}}\; м/с = 16,67\; м/с \]
В итоге:
\[S = \frac{{{{16,67}^2}}}{{2 \cdot 3}} = 46,30\; м \]
Ответ: 46,30 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.11 Автобус движется равнозамедленно, проходя при этом до остановки расстояние
1.3.13 Машинист локомотива, движущегося со скоростью 72 км/ч, начал тормозить
1.3.14 Поезд, имеющий скорость 90 км/ч, стал двигаться с замедлением 0,3 м/с2. Найти
Почему нельзя через формулу:
v0+a×t=0.
v0= 60 км/сек= 60 × 1000 ÷ 3600 м/сек = 50 м/с
50÷3-3×t=0
t = 50/9
S= v0×t +a×t^2÷2 = 2500÷27-50÷6=84+7÷27
И когда используется формула которую вы использовали…
Помогите пожалуйста…