Условие задачи:
В горизонтальном направлении со скоростью 10 м/с брошено тело, которое падает на землю через 3 с. Найдите тангенс угла, который составит вектор скорости тела с горизонтом при падении.
Задача №1.5.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=10\) м/с, \(t=3\) с, \(tg \alpha-?\)
Решение задачи:
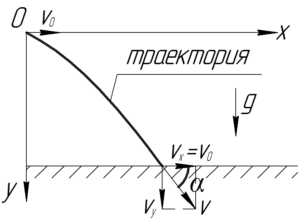 Если разложить вектор скорости тела при падении на горизонтальную \(\upsilon_x\) и вертикальную \(\upsilon_y\) составляющие, то вопрос задачи можно переформулировать иначе, а именно так, что нам нужно найти тангенс угла между \(\upsilon_x\) и \(\upsilon\) (смотри рисунок). Для этого никуда не деться от того, что записать уравнения скорости в проекциях на введенные нами оси \(x\) и \(y\).
Если разложить вектор скорости тела при падении на горизонтальную \(\upsilon_x\) и вертикальную \(\upsilon_y\) составляющие, то вопрос задачи можно переформулировать иначе, а именно так, что нам нужно найти тангенс угла между \(\upsilon_x\) и \(\upsilon\) (смотри рисунок). Для этого никуда не деться от того, что записать уравнения скорости в проекциях на введенные нами оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:{\upsilon _x} = {\upsilon _0}\,\,\,(1) \hfill \\
oy:{\upsilon _y} = gt\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Искомый тангенс согласно рисунку равен следующему отношению:
\[{\text{tg}}\alpha = \frac{{{\upsilon _y}}}{{{\upsilon _x}}}\]
Иcпользуя формулы (1) и (2), окончательно формула для нахождения тангенса будет равна:
\[{\text{tg}}\alpha = \frac{{gt}}{{{\upsilon _0}}}\]
Осталось подставить численно исходные данные в формулу и сосчитать ответ:
\[{\text{tg}}\alpha = \frac{{10 \cdot 3}}{{10}} = 3\]
Ответ: 3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.5.2 Камень брошен с некоторой высоты в горизонтальном направлении и упал
1.5.4 Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с
1.5.5 Два тела брошены с высоты 100 м, первое — с горизонтальной скоростью 5 м
В задаче 1.5.4 ox:x=υ_0*t ; oy:y=gt^2/2 . а тут ox:u_x=υ_0 ; oy:u_y=gt
почему это так
Там координаты, тут скорости
Почему в задаче 1.5.2 tg a=Vx/Vy , а в этой наоборот.
Если Вы внимательно посмотрите рисунки к этой задаче и к задаче 1.5.2, то увидите, что углом α обозначены разные углы, поэтому и формулы для вычисления тангенса разные.
А почему мы взяли разные углы?
В задаче 1.5.2 в условии дан угол между скоростью и вертикалью, здесь же в условии просят найти угол между скоростью и горизонталью, поэтому углы и разные.
υ0=gt⋅tgα
Если оттуда выразить tgα, то получится tgα=υ0/gt, Или я ошибаюсь?
Ошибаетесь, чтобы Ваша формула была верна, то в ней должен быть котангенс, а не тангенс.
Смотрите моё решение, там всё верно