Условие задачи:
 С какой скоростью будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью 1 см/с, а катушка катится без скольжения. Радиус внутренней части катушки \(r=2\) см, внешней — \(R=3\) см.
С какой скоростью будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью 1 см/с, а катушка катится без скольжения. Радиус внутренней части катушки \(r=2\) см, внешней — \(R=3\) см.
Задача №1.8.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=1\) см/с, \(r=2\) см, \(R=3\) см, \(\upsilon_1-?\)
Решение задачи:
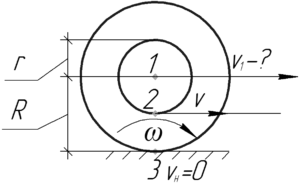 Скорость той точки катушки (точка 2), с которой начинается горизонтальный отрезок нити, такая же как у нити, то есть \(\upsilon\). Если катушка катится без проскальзывания, то скорость точки (точка 3), которая соприкасается со столом, равна нулю. Более подробно причины этого описаны здесь. То есть эта точка является мгновенным центром скоростей (МЦС), а значит в это мгновение все точки катушки совершают вращательное движение с угловой скоростью \(\omega\) вокруг МЦС. Тогда справедливо записать:
Скорость той точки катушки (точка 2), с которой начинается горизонтальный отрезок нити, такая же как у нити, то есть \(\upsilon\). Если катушка катится без проскальзывания, то скорость точки (точка 3), которая соприкасается со столом, равна нулю. Более подробно причины этого описаны здесь. То есть эта точка является мгновенным центром скоростей (МЦС), а значит в это мгновение все точки катушки совершают вращательное движение с угловой скоростью \(\omega\) вокруг МЦС. Тогда справедливо записать:
\[\left\{ \begin{gathered}
\upsilon = \omega \left( {R — r} \right) \hfill \\
{\upsilon _1} = \omega R \hfill \\
\end{gathered} \right.\]
Делим нижнее выражение на верхнее и выражаем искомую скорость \(\upsilon_1\).
\[\frac{{{\upsilon _1}}}{\upsilon } = \frac{R}{{R — r}} \Rightarrow {\upsilon _1} = \frac{{\upsilon R}}{{R — r}}\]
Остается только вычислить ответ.
\[{\upsilon _1} = \frac{{1 \cdot 3}}{{3 — 2}} = 3\; см/с = 0,03\; м/с = 0,11\; км/ч\]
Интересно, что многие скажут, что катушка в таком опыте покатится влево. На самом деле она будет катиться вправо. Дело в том, что катушка катится туда, куда направлена угловая скорость \(\omega\). Такой эксперимент сложно повторить, не нарушая условий, а именно, условие отсутствия скольжения катушки.
Также интересно, что нить будет наматываться на катушку, так как \({\upsilon _1} > \upsilon\). Объясняется это тем, что скорость точки 2 (а значит и скорость нити) в системе отсчета катушки направлена влево.
Ответ: 0,11 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.29 Точка движется по окружности с постоянной по величине скоростью 50 см/с
1.8.31 Стержень длиной 50 см вращается с частотой 30 об/мин вокруг перпендикулярной
1.8.32 Гладкий горизонтальный диск вращается вокруг вертикальной оси с частотой
А если нить тянуть под углом к горизонту? Или вертикально вверх?
У меня такие мысли. Если размышлять формально, то скорость у точки 2 катушки в таком случае также будет равна \(\upsilon\). Но в таком случае будет очень тяжело соблюсти условие качение без скольжения. Да и если нить тянуть не горизонтально, а под углом или вертикально вверх, то вероятно, что усложнять движение катушки будет та же самая нить.
Ничего сложного в решении задачи, если нить тянуть под углом к горизонту… Это обычная задача курса «Теоретическая механика» технического университета…
«Но в таком случае будет очень тяжело соблюсти условие качение без скольжения» — что-то не наблюдаю такого в задачах курса «Теоретическая механика»…
А как определить в какую сторону направлена угловая скорость? Ведь при натяжении нити в точке 2 мы придаем вращательное движение катушки против часовой стрелки, следовательно и угловая скорость вращения катушки направлена справа налево.
Я не понимаю как в данном случае определить в какую сторону будет двигаться катушка.
Катушка катится вправо, поэтому она вращается по часовой стрелке.
Так если она катиться вправо, то она будет наматывать нить (если потянуть и отпустить) или будет проскальзывать на месте, возможно сдвинется с места вправо, что противоречит условию. Если бы мы тянули нить сверху, тогда да, катушка будет двигаться вправо.
Понимаю, что это контринтуитивно, но так оно и есть. Если не доверяете мне, то можете прочитать решение этой задачи в «Гельфгат И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с решением», приведенная задача имеет номер 1.57. В конце указанного сборника приведено подробное решение.
ДА… будет наматываться нить…
и ничего в этом удивительного нет…
Всё остальное про проскальзывание… — не понимание механики…
В решении задачи упущено указание, что точка «3» — МСЦ (мгновенный центр скоростей)
…а далее всё просто…
υ1=ωR согласен
υ=ω(R—r) разве не будет верно, υ=ωr ?
Вы можете утверждать, что скорость точки 1 в СО Земли равна скорости точки 3 в СО катушки, поскольку нет проскальзывания. Скорость точки 2 же при переходе из одной СО в другую будет меняться, и эти скорости (т.е. скорости точки 2 в разных СО) будут равны лишь при случае r=R/2.
Так что нет, все-таки υ=ωr — это неправильно.