Условие задачи:

Под каким углом к горизонту нужно бросить тело, чтобы высота его подъема была в два раза больше дальности его полета?

Задача №1.6.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$H=2L$, $\alpha-?$

Решение задачи:

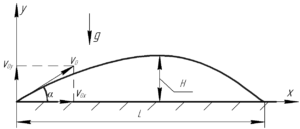Для лучшего понимания хода решения задачи представим к ней рисунок, он показан вам справа. Как и во всех задачах на бросание тела под углом к горизонту запишем уравнения движения тела в проекциях на оси координат $x$ и $y$.

$$\left\{ \begin{gathered} ox:\,\,x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\ oy:\,\,y = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\,\,(2) \hfill \\ \end{gathered} \right.$$

Определим время полета, приравняв второе уравнение к нулю.

$$y = 0 \Rightarrow {v_0}\sin \alpha  \cdot t — \frac{{g{t^2}}}{2} = 0$$

Получаем два корня, первый из которых нам не интересен.

$$\left[ \begin{gathered} t = 0 \hfill \\ t = \frac{{2{v_0}\sin \alpha }}{g} \hfill \\ \end{gathered} \right.$$

Подставив второй корень в уравнение (1) мы получаем формулу для определения дальности полета.

$$L = \frac{{2v_0^2\sin \alpha \cos \alpha }}{g}$$

Теперь разберемся с высотой подъема. В наивысшей точке полета вертикальная составляющая скорости становится равной нулю. Поэтому запишем уравнения скорости движения тела в проекции на обе оси.

$$\left\{ \begin{gathered} ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\ oy:{v_y} = {v_0}\sin \alpha — gt\,\,(4) \hfill \\ \end{gathered} \right.$$

Пользуясь вышесказанным, из уравнения (4) найдем время подъема.

$${v_y} = 0 \Rightarrow {v_0}\sin \alpha  — g{t_1} = 0$$

$${t_1} = \frac{{{v_0}\sin \alpha }}{g}$$

Кстати, время подъема можно было найти гораздо легче, просто поделив найденное общее время на 2. Подставим его в уравнение (2), в итоге имеем формулу для определения высоты подъема.

$$H = {v_0}\sin \alpha  \cdot \frac{{{v_0}\sin \alpha }}{g} — \frac{g}{2}{\left( {\frac{{{v_0}\sin \alpha }}{g}} \right)^2} = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}$$

Теперь нужно вспомнить, что в задании дано условие $H=2L$, подставим в него полученные нами формулу.

$$H = 2L$$

$$\frac{{v_0^2{{\sin }^2}\alpha }}{{2g}} = \frac{{4v_0^2\sin \alpha \cos \alpha }}{g}$$

Из этого равенства имеем, что:

$$\operatorname{tg} \alpha  = 8 \Rightarrow \operatorname{arctg} \alpha  = 82,87^\circ$$

Ответ: 82,87°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.5 На некоторой высоте одновременно из одной точки брошены
1.6.7 Мяч, брошенный под некоторым углом к горизонту с начальной
1.6.8 Мяч, брошенный со скоростью 10 м/с под углом 45 градусов