Условие задачи:
На какую высоту поднимется тело, брошенное вертикально вверх с начальной скоростью 800 м/с. Сопротивлением воздуха пренебречь.
Задача №1.4.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=800\) м/с, \(h-?\)
Решение задачи:
Первый способ решения — длинный.
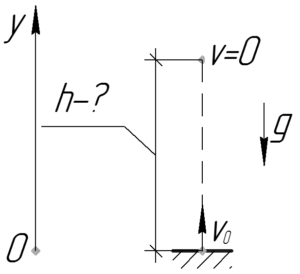
Тело бросают вертикально вверх с начальной скоростью, из-за ускорения свободного падения оно равно или поздно достигнет максимально высоты, остановится и устремится обратно к земле. Для того, чтобы определить эту высоту запишем уравнения движения и уравнение скорости тела:
\[oy:y = {\upsilon _0}t — \frac{{g{t^2}}}{2}\;\;\;\;(1)\]
\[oy:\upsilon = {\upsilon _0} — gt\;\;\;\;(2)\]
В точке максимального подъема скорость тела \(\upsilon\) равна нулю. Из выражения (2) определим время полета:
\[\upsilon = 0 \Rightarrow 0 = {\upsilon _0} — gt \Rightarrow t = \frac{{{\upsilon _0}}}{g}\]
Подставим полученную формулу в выражение (1):
\[h = \frac{{\upsilon _0^2}}{g} — \frac{g}{2}\frac{{\upsilon _0^2}}{{{g^2}}} = \frac{{\upsilon _0^2}}{{2g}}\]
Второй способ решения — короткий.
Используем известную формулу без времени (знак «минус» справа присутствует из-за того, что движение замедленное!):
\[{\upsilon ^2} — \upsilon _0^2 = — 2gh\]
Конечная скорость \(\upsilon\) равна нулю, поэтому формула станет короче. Выразим оттуда искомую высоту \(h\).
\[\upsilon _0^2 = 2gh \Rightarrow h = \frac{{\upsilon _0^2}}{{2g}}\]
Видно, что если в задаче не дано времени, то лучше использовать второй способ.
Подсчитаем ответ:
\[h = \frac{{{{800}^2}}}{{2 \cdot 10}} = 32000\; м = 32\; км\]
Ответ: 32 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.2 Высота свободного падения молота 2,5 м. Определить его скорость
1.4.4 Тело брошено вертикально вверх со скоростью 50 м/с. Через какое время
1.4.5 При свободном падении время полета первого тела больше в 2 раза, чем
помогите пожалуйста решить задачи:
1) Определите на какую максимальную высоту поднимется тело, если его подбросили вертикально вверх со скоростью 30 м/с.
2) Определите скорость пули через 2,5 с после выстрела вертикально вверх, если скорость в момент вылета из ствола была 300 м/с.
1) Используем формулу кинематики без времени: \[{\upsilon ^2} — \upsilon _0^2 = — 2gH\]На максимальной высоте скорость тела будет равна нулю, тогда:\[\upsilon _0^2 = 2gH\]Максимальная высота равна:\[H = \frac{{\upsilon _0^2}}{{2g}}\]\[H = \frac{{{{30}^2}}}{{2 \cdot 10}} = 45\;м\]
2) Скорость пули в любой момент, движущейся вертикально вверх, можно найти по формуле:\[\upsilon = {\upsilon _0} — gt\]\[\upsilon = 300 — 10 \cdot 2,5 = 275\;м/с\]
Спасибо за ответ я понял как теперь решать

Можете сказать название формулы, использованной в первом шаге второго способа?υ
v2—v02=—2gh
По сути это закон сохранения энергии Ещё называют формулой кинематики без времени
Ещё называют формулой кинематики без времени
Я взял формулу h_max = v_0^2*sin^2a/2*g a = 90. У меня вышло тот же самый ответ только, боюсь что я взял не правильную формулу. Или нет?
Да, Вы взяли формулу максимальной высоты для тела, брошенного под углом к горизонту, а в задаче тело брошено вертикально вверх. Правильная формула показана в решении выше (как и вывод этой формулы).
у меня вместо формул что-то вроде {{{70}^2}}}}{{{{\56\2{}[]
Для корректного отображения формул на сайте в браузере должны быть разрешены запуски скриптов js
С какой максимальной скоростью человек может бросить камень или мячик своей рукой?
Для решения задачи используем информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек. Масса бейсбольного мяча известна и приближенно равна m = 0,145 кг. Соответствующую кинетическую энергию (Е), затраченную на бросок мяча рукой, оценим из формулы Е ≈ (δМ + m)v²/2, где М — масса человека, а δМ = 0,005М — масса кисти руки.
Подставив в формулу массу среднего человека, M ≈ 70 кг, получим, что энергия рекордного броска равнялась E ≈ 500 Дж. Зафиксировав это значение как предел, решим теперь задачу в обратном направлении — найдём приближённую формулу для максимальной скорости (v) произвольного предмета с массой m, брошенного человеком с массой М, при фиксированной максимальной энергии E = 500 Дж.
Ответ: v ≈ √{2E/(δМ + m)} ≈ √{1000/(0,005М + m)}, [м/сек], где m и М в единицах кг. Подставив числовые значения, определим скорость,с которой человек может кинуть бейсбольный мяч. V= √1000/0.005×70+0.145=45 м/с=162км/ч
Можно сказать,что проверили информацию о рекордной скорости бейсбольного мяча на подаче, равный v ≈ 45 м/сек.
В газете прочитал такую статью: «Насколько высоко человек может что-либо подбросить?. Возьмем,например, бейсбольный мяч.Питчер, кидающий фастбол на скорости 130 км/, сумеет добросить его до высоты 50 метров. Я решил взять вышеуказанную задачу и проверить результат в 50 метров. Перевел в м/с: 130 км/час=36м/с
Выбрав вторую формулу, находим h=36^2/2×10=64.8 метра.
Правильно я проверил?
Думаю, да.
Проблема в том, что питчер не кидает мяч вертикально вверх, а формула справедлива только для мяча, брошенного вертикально вверх.
У меня получилось вот так:
Уравнение движения тела y = v_0 * t — (g * t^2 )/2. (*)
Время t можно найти из этого уравнения g = (v — v_0)/t => t = (v — v_0)/g. t = 81,6c
Подставим все известные значения в уравнение (*) и получим y = 32653 м.
Разница между вашими моим ответом 653 м.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
В решении я принял, что \(g = 10\;м/с^2\), а у Вас по всей видимости \(g = 9,81\;м/с^2\). Разница в 600 с лишним метров в таком случае нормальна. Это всего лишь 2% от 32000 м.
Ваше решение тоже правильно (как и моё), хотя мне не нравится один момент. Вы решает по действиям и накапливаете ошибку. Если использовать мою конечную формулу и принять \(g = 9,81\;м/с^2\), то:
\[h = \frac{{{{800}^2}}}{{2 \cdot 9,81}} = 32619,8\;м\]
Тогда у нас с Вами разница 40 м, а её вообще не должно быть.