Условие задачи:

Мяч брошен вверх со скоростью 10 м/с. На каком расстоянии от поверхности Земли он будет находиться через 2 с?

Задача №1.4.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon_0=10$ м/с, $t=2$ с, $h-?$

Решение задачи:

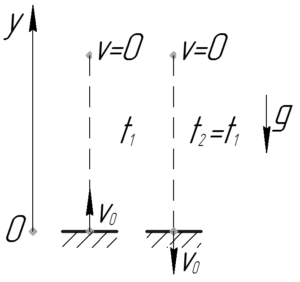Пойдем нестандартным путем. Определим, сколько времени $t_1$ тело будет двигаться до точки максимального подъема, для этого запишем уравнение скорости мяча в проекции на ось $y$.

$$oy:\upsilon  = {\upsilon _0} — gt$$

В наивысшей точке скорость мяча $\upsilon$ равна нулю.

$$\upsilon  = 0 \Rightarrow 0 = {\upsilon _0} — g{t_1} \Rightarrow {t_1} = \frac{{{\upsilon _0}}}{g}$$

$${t_1} = \frac{{10}}{{10}} = 1\; с$$

Но мы знаем, что время подъема тела и время его падения равны, значит, что тело окажется опять на Земле, то есть через 2 секунды расстояние от Земли станет равным нулю.

Можно пойти и обычным путем, для этого нужно лишь записать уравнение движения мяча вдоль оси $y$.

$$oy:y = {\upsilon _0}t — \frac{{g{t^2}}}{2}$$

В любой момент времени $t$ координата мяча $y$ показывает расстояние мяча от Земли, при этом неважно, что тело после достижения максимальной точки подъема станет двигаться вниз, и ускорение свободного падения станет разгонять тело. Уравнение никак не нужно переписывать для устранения этого несоответствия.

$$h = {\upsilon _0}t — \frac{{g{t^2}}}{2}$$

$$h = 10 \cdot 2 — \frac{{10 \cdot {2^2}}}{2} = 0\; м$$

Ответ: 0 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.11 Камень, брошенный вертикально вверх со скоростью 12 м/с, через 1 с
1.4.13 Мяч брошен с некоторой высоты вертикально вниз со скоростью 5 м/с. Какова
1.4.14 Мяч брошен вверх со скоростью 20 м/с. На какое расстояние от поверхности