Условие задачи:
Мяч брошен с земли вертикально вверх. На высоте 10 м он побывал два раза с интервалом времени 2,83 с. Определить начальную скорость бросания мяча.
Задача №1.4.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=10\) м, \(\Delta t=2,83\) с, \(\upsilon_0-?\)
Решение задачи:
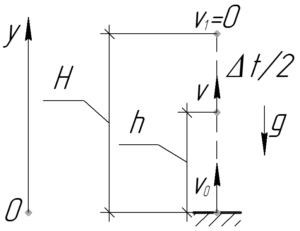 Давайте рассмотрим движение мяча после того, как он достиг высоты 10 м в первый раз. В этой точке у мяча, естественно, будет какая-то отличная от нуля скорость, но сколько он будет двигаться до наивысшей точки? Правильный ответ на этот вопрос — половина данного в условии интервала времени, т.е. \(\frac{\Delta t}{2}\). Получается, что мы можем узнать какую скорость \(\upsilon\) имеем мяч на высоте в 10 м из условия, что в наивысшей точке его скорость равна нулю.
Давайте рассмотрим движение мяча после того, как он достиг высоты 10 м в первый раз. В этой точке у мяча, естественно, будет какая-то отличная от нуля скорость, но сколько он будет двигаться до наивысшей точки? Правильный ответ на этот вопрос — половина данного в условии интервала времени, т.е. \(\frac{\Delta t}{2}\). Получается, что мы можем узнать какую скорость \(\upsilon\) имеем мяч на высоте в 10 м из условия, что в наивысшей точке его скорость равна нулю.
\[0 = \upsilon — g\frac{{\Delta t}}{2} \Rightarrow \upsilon = g\frac{{\Delta t}}{2}\]
Теперь мы можем узнать до какой максимальной высоты поднялось тело, а для этого запишем уравнение движения тела.
\[oy:y = h + \upsilon t — \frac{{g{t^2}}}{2}\]
Через время \(t=\frac{\Delta t}{2}\) координата \(y\) станет равной максимальной высоте подъема мяча \(H\).
\[H = h + \upsilon \frac{{\Delta t}}{2} — \frac{g}{2}\frac{{\Delta {t^2}}}{4}\]
Подставим в формулу известную нам скорость \(\upsilon\).
\[H = h + g\frac{{\Delta t}}{2}\frac{{\Delta t}}{2} — \frac{g}{2}\frac{{\Delta {t^2}}}{4} = h + \frac{{g\Delta {t^2}}}{8}\]
Осталось только воспользоваться очень хорошей формулой:
\[\upsilon _1^2 — \upsilon _0^2 = — 2gH\]
Здесь \(\upsilon_1\) — это скорость мяча на высоте \(H\), которая равна нулю, \(\upsilon_0\) — скорость мяча при броске. Знак «минус» в правой части говорит о том, что движение мяча является равнозамедленным. В итоге имеем:
\[\upsilon _0^2 = 2gH\]
\[{\upsilon _0} = \sqrt {2g\left( {h + \frac{{g\Delta {t^2}}}{8}} \right)} \]
Подсчитаем численный ответ.
\[{\upsilon _0} = \sqrt {2 \cdot 10\left( {10 + \frac{{10 \cdot {{2,83}^2}}}{8}} \right)} = 20\; м/с \]
Ответ: 20 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.19 Камень упал в шахту. Определить глубину шахты, если звук от падения камня
1.4.21 Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени
1.4.22 Тело, брошенное вертикально вверх, за третью секунду прошло 5 м. Определить
ЭДС батарейки карманного фонарикаравна3, 7В,внутреннее сопротивление 1,5ОМ.Батарейка замкнута на сопротивление 11,7ОМ.Каково напряжение на зажима батарейки?
…опечатка…
(V0^2 – V_h^2) / (2 g) = h
V0 = …
V_h = g Δt / 2
1) можно воспользоваться законом сохранения энергии
m V0^2 / 2 = m g h + m V_h^2 / 2
V0 = …
2) можно сразу написать:
(V_h^2 — V0^2) / (2 g) = h
V0 = …
!!!
А зачем находим высоту H ?
В задаче это не требуется…
Это такое класное чуство, когда решаешь какую-то задачу))) Раньше я не мог даже элементарную задачу решить. Я не говорю, что эта сложная, но я был просто нулём, а теперь мой учитель физики готовит меня к защите проекта! Спасибо автору сайта за то, что дал возможность попрактиковаться и научится новому!
Не за что

Спасибо за отзыв, очень приятно!
спс