Условие задачи:

Камень брошен с некоторой высоты в горизонтальном направлении и упал на Землю через 3 с под углом 60° к вертикали. Определить начальную скорость камня.

Задача №1.5.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(t=3\) с, \(\alpha=60^\circ\), \(\upsilon_0-?\)

Решение задачи:

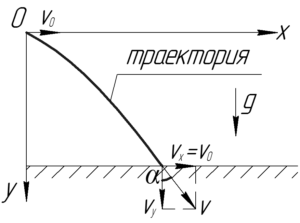Давайте в начале поясним, что означает предложение «камень упал под таким-то углом к вертикали», ведь вроде камень — это материальная точка, и если это так, то как можно связать точку с углом. На самом деле данный угол 60° — это угол между вектором скорости камня за мгновение до удара о землю и вертикалью. Напомним, что вектор скорости лежит на касательной к траектории в точке соприкосновения с землей. Все эти факты отлично проиллюстрированы на рисунке справа.

Запишем уравнения скорости в проекциях на оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:{\upsilon _x} = {\upsilon _0}\,\,\,(1) \hfill \\
oy:{\upsilon _y} = gt\,\,\,(2) \hfill \\
\end{gathered} \right.\]

В точке удара камня о землю мы разложили его скорость на составляющие \(\upsilon_x\) и \(\upsilon_y\). Значит угол \(\alpha\) это еще и угол между вертикальной составляющей скорости и ее полной величиной.

Выразим тангенс этого угла:

\[{\text{tg}}\alpha  = \frac{{{\upsilon _x}}}{{{\upsilon _y}}}\]

Учитывая выражения (1) и (2) также справедливо:

\[{\text{tg}}\alpha  = \frac{{{\upsilon _0}}}{{gt}}\]

В итоге искомое \(\upsilon_o\) можно найти из формулы:

\[{\upsilon _0} = gt \cdot {\text{tg}}\alpha \]

Подставим исходные данные численно и сосчитаем ответ:

\[{\upsilon _0} = 10 \cdot 3 \cdot {\text{tg60}}^\circ  = 51,96 \; м/с = 187\; км/ч \]

Ответ: 187 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.5.1 Камень брошен горизонтально со скоростью 5 м/с. Через 0,8 с он упал
1.5.3 В горизонтальном направлении со скоростью 10 м/с брошено тело, которое
1.5.4 Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с