Условие задачи:
Из точки A вертикально вверх брошено тело с начальной скоростью 10 м/с. Когда оно достигло высшей точки своей траектории, из точки A бросают вертикально вверх тело с начальной скоростью 20 м/с. Через какое время после начала движения второго тела произойдет встреча этих тел?
Задача №1.4.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_{01}=10\) м/с, \(\upsilon_{02}=20\) м/с, \(t_2-?\)
Решение задачи:
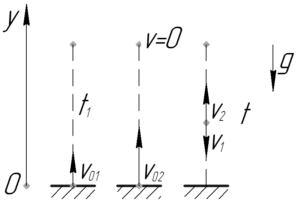 Запишем уравнения движения данных двух тел в проекции на ось \(y\). При этом учтем, что второе тело начинает двигаться позднее, через время \(t_1\), необходимое первому телу для достижения наивысшей точки подъема.
Запишем уравнения движения данных двух тел в проекции на ось \(y\). При этом учтем, что второе тело начинает двигаться позднее, через время \(t_1\), необходимое первому телу для достижения наивысшей точки подъема.
\[\left\{ \begin{gathered}
oy:y = {\upsilon _{01}}t — \frac{{g{t^2}}}{2} \hfill \\
oy:y = {\upsilon _{02}}\left( {t — {t_1}} \right) — \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]
Найдем время \(t_1\), для этого запишем уравнение скорости первого тела, спроецированное на ось \(y\). В верхней точке его скорость будет равна нулю, поэтому верно следующее.
\[\upsilon = {\upsilon _{01}} — gt_1\]
\[\upsilon = 0 \Rightarrow {t_1} = \frac{{{\upsilon _{01}}}}{g}\]
Когда два тела встретятся, их координаты будут равны, поэтому приравняем оба уравнения, которые мы записали в системе, раскроем скобки и перенесем слагаемые с неизвестным \(t\) в одну сторону.
\[{\upsilon _{02}}\left( {t — {t_1}} \right) — \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} = {\upsilon _{01}}t — \frac{{g{t^2}}}{2}\]
\[{\upsilon _{02}}t — {\upsilon _{02}}{t_1} — \frac{{g{t^2}}}{2} + gt{t_1} — \frac{{gt_1^2}}{2} = {\upsilon _{01}}t — \frac{{g{t^2}}}{2}\]
\[t\left( {{\upsilon _{02}} — {\upsilon _{01}} + g{t_1}} \right) = {\upsilon _{02}}{t_1} + \frac{{gt_1^2}}{2}\]
Нам уже известно, что \({t_1} = \frac{{{\upsilon _{01}}}}{g}\), поэтому:
\[t\left( {{\upsilon _{02}} — {\upsilon _{01}} + g\frac{{{\upsilon _{01}}}}{g}} \right) = {\upsilon _{02}}\frac{{{\upsilon _{01}}}}{g} + \frac{g}{2}\frac{{\upsilon _{01}^2}}{{{g^2}}}\]
\[t \cdot {\upsilon _{02}} = \frac{{{\upsilon _{01}} \cdot {\upsilon _{02}}}}{g} + \frac{{\upsilon _{01}^2}}{{2g}}\]
\[t = \frac{{{\upsilon _{01}}}}{g} + \frac{{\upsilon _{01}^2}}{{2g{\upsilon _{02}}}}\]
Отлично, но мы нашли формулу для вычисления времени до встречи, отсчитываемое от момента броска первого тела. Поэтому, если мы хотим найти время \(t_2\) от момента броска второго тела до встречи двух тел в воздухе, то воспользуемся формулой:
\[{t_2} = t — {t_1}\]
\[{t_2} = \frac{{{\upsilon _{01}}}}{g} + \frac{{\upsilon _{01}^2}}{{2g{\upsilon _{02}}}} — \frac{{{\upsilon _{01}}}}{g} = \frac{{\upsilon _{01}^2}}{{2g{\upsilon _{02}}}}\]
Подставим числа и сосчитаем ответ:
\[{t_2} = \frac{{{{10}^2}}}{{2 \cdot 10 \cdot 20}} = 0,25\; с = 250\; мс\]
Ответ: 250 мс.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.17 Камень, брошенный вертикально вверх, упал на Землю через 2 с. Определить
1.4.19 Камень упал в шахту. Определить глубину шахты, если звук от падения камня
1.4.20 Мяч брошен с земли вертикально вверх. На высоте 10 м он побывал два раза
υ=υ01—gt
υ=0⇒t1=υ01g
Почему t1,если в формуле t?
Подправил решение, спасибо за замечание!
А почему в первом уравнении системы y = V01 * t — g*t^2 / 2/
Кажется должно быть y = V01*t + gt^2/2
Почему? Скорость v01 сонаправлена с направлением оси y, а ускорение свободного падения g — противонаправлена, поэтому в решении все написано верно
А можно найти и так: h01=10*1-10*1/2=10-5=5 and h02=20(2-2)-10*(2-1)^2/2=20*1-(10*3)/2=5 =>:t=h01/v01=5/10=0,5c and t2=h02/v02=5/20=0,25c theend.
Вы проверяете моё решение? Или решаете методом подбора?
Физику не решают методом подбора. Для математики, конечно, навык очень полезный и необходимый. Но не для физики.
Я вам запросто подберу такие исходные данные, при которых Вы не сможете подобрать решение (например, подберу дробное решение уравнения).