Условие задачи:

Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода с начальной скоростью 10 м/с. Площадь сечения 5 см². Определить массу струи, находящейся в воздухе.

Задача №1.6.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=45^\circ\), \(v_0=10\) м/с, \(S=5\) см², \(m-?\)

Решение задачи:

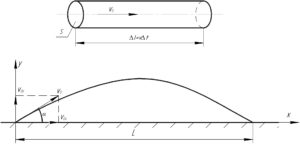Общий принцип решения задач про струи воды в воздухе уже был описан в данной задаче (для лучшего понимания прочтите ее) и заключается в том, что каждую секунду из шланга выходит один и тот же объем (а, следовательно, и масса) воды, а значит для нахождения массы струи, находящейся в воздухе, достаточно знать время полета. Рисунок к решению представлен справа, клик по нему увеличивает его.

Все сказанное выражается формулой:

\[m = \rho V = \rho S{v_0}t\]

Далее все сводится к обычной кинематике, поэтому запишем уравнения движения первой вышедшей из шланга малой порции воды:

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\,\,(2) \hfill \\
\end{gathered} \right.\]

Когда первая порция воды достигнет земли, то ее координата \(y\) станет равной нулю, поэтому приравняем уравнение (2) к нулю и найдем оба корня квадратного уравнения.

\[y = 0 \Rightarrow {v_0}\sin \alpha  \cdot t — \frac{{g{t^2}}}{2} = 0\]

\[t\left( {{v_0}\sin \alpha {\text{ }} — \frac{{gt}}{2}} \right) = 0\]

Очевидно, корни этого уравнения следующие:

\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{v_0}\sin \alpha }}{g} \hfill \\
\end{gathered} \right.\]

Первый корень нам не интересен. Подставим второй корень в самую первую формулу и получаем ответ в общем виде:

\[m = \rho S\frac{{2v_0^2\sin \alpha }}{g}\]

Подставим все известные данные в СИ и получим ответ:

\[m = 1000 \cdot 5 \cdot {10^{ — 4}} \cdot \frac{{2 \cdot {{10}^2} \cdot \sin 45^\circ }}{{10}} = 7,07\; кг\]

Ответ: 7,07 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.16 Из орудия сделан выстрел вверх по склону горы. Угол наклона горы
1.6.18 Какое расстояние по горизонтали до первого удара о пол
1.6.19 Какой скоростью обладал мальчик при прыжке с трамплина