Условие задачи:

Из орудия сделан выстрел вверх по склону горы. Угол наклона горы к горизонту 30°, угол наклона ствола орудия к горизонту 60°, скорость вылета снаряда 21 м/с. Найти расстояние от орудия до точки падения снаряда вдоль склона горы (\(g=9,8\) м/с².)

Задача №1.6.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\beta=60^\circ\), \(v_0=21\) м/с, \(g=9,8\) м/с², \(S-?\)

Решение задачи:

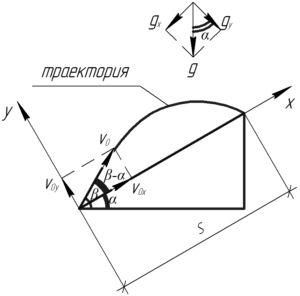Во всех задачах, где рассматривается движение тела вдоль какой-то наклонной плоскости, лучше вводить оси \(x\) и \(y\) вдоль и перпендикулярно этой плоскости соответственно. Подобная задача уже разбиралась на нашем сайте, она немного сложнее, поэтому если вы хотите усвоить этот прием лучше, то желательно посмотреть и ее. Рисунок, показывающий решение задачи, приведен справа.

Запишем уравнения движения снаряда в проекциях на введенные нами \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos (\beta — \alpha ) \cdot t — \frac{{g\sin \alpha \cdot {t^2}}}{2}\,\,\,(1) \hfill \\
oy:y = {v_0}\sin (\beta — \alpha ) \cdot t — \frac{{g\cos \alpha \cdot {t^2}}}{2}\,\,(2) \hfill \\
\end{gathered} \right.\]

В момент касания холма координата \(y\) снаряда станет равной нулю, приравняем уравнение (2) к нулю.

\[y = 0 \Rightarrow {v_0}\sin (\beta  — \alpha ) \cdot t — \frac{{g\cos \alpha  \cdot {t^2}}}{2} = 0\]

\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{v_0}\sin (\beta — \alpha )}}{{g\cos \alpha }} \hfill \\
\end{gathered} \right.\]

Первый корень соответствует моменту запуска снаряда, он нас не интересует. Второй корень подставим в уравнение (1).

\[S = {v_0}\cos (\beta  — \alpha ) \cdot t — \frac{{g\sin \alpha  \cdot {t^2}}}{2}\]

\[S = {v_0}\cos (\beta  — \alpha ) \cdot \frac{{2{v_0}\sin (\beta  — \alpha )}}{{g\cos \alpha }} — \frac{{g\sin \alpha }}{2}\frac{{4v_0^2{{\sin }^2}(\beta  — \alpha )}}{{{g^2}{{\cos }^2}\alpha }}\]

\[S = \frac{{2v_0^2\sin (\beta  — \alpha )\cos (\beta  — \alpha )}}{{g\cos \alpha }} — \frac{{2v_0^2{{\sin }^2}(\beta  — \alpha )\sin \alpha }}{{g{{\cos }^2}\alpha }}\]

Окончательная формула для решения задачи в общем виде имеет вид:

\[S = \frac{{2v_0^2\sin (\beta  — \alpha )}}{{g\cos \alpha }}\left( {\cos (\beta  — \alpha ) — \frac{{\sin (\beta  — \alpha )\sin \alpha }}{{\cos \alpha }}} \right)\]

Подставим все известные в системе измерения СИ и получим ответ:

\[S = \frac{{2 \cdot {{21}^2} \cdot \sin (60^\circ  — 30^\circ )}}{{9,8 \cdot \cos 30^\circ }}\left( {\cos (60^\circ  — 30^\circ ) — \frac{{\sin (60^\circ  — 30^\circ )\sin 30^\circ }}{{\cos 30^\circ }}} \right) = 30\; м.\]

Ответ: 30 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.15 Камень, брошенный под углом к горизонту, упал на землю
1.6.17 Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода
1.6.18 Какое расстояние по горизонтали до первого удара о пол