Условие задачи:
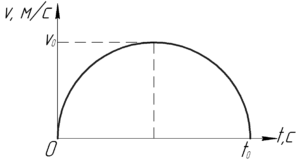График зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела \(\upsilon_0\), время движения \(t_0\). Определить путь, пройденный телом. Рисунок, приведенный в условии задачи, изображен справа.
Задача №1.1.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0\), \(t_0\), \(S-?\)
Решение задачи:
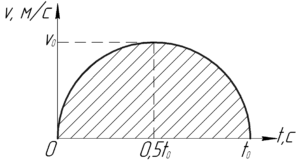Также, как и во втором способе решения этой задачи, используем тот факт, что путь, пройденный телом, возможно определить как площадь фигуры под графиком зависимости скорости тела от времени (на рисунке к решению заштриховано). Так как график имеет вид полуокружности, то и его площадь находится как половина площади круга:
\[S = \frac{1}{2}\pi {r^2}\]
Запишем формулу в такой форме:
\[S = \frac{1}{2}\pi r \cdot r\]
Это необходимо для того, чтобы человек, решающий эту задачу не подставил вместо \(r\) либо только \(\upsilon_0\), либо только \(\frac{t_0}{2}\), поскольку в таком случае ответ не будет подходить по размерности с размерностью пути. Поэтому, вместо первого \(r\) подставим \(\upsilon_0\), а вместо второго – \(\frac{t_0}{2}\). Только в этом случае мы сможем получить верный ответ:
\[S = \frac{1}{2}\pi {\upsilon _0} \cdot \frac{{{t_0}}}{2} = 0,25\pi {\upsilon _0}{t_0}\]
Ответ: \(0,25\pi {\upsilon _0}{t_0}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.1.3 Скорость тела меняется по закону v=10+2t. Чему равен путь, пройденный
1.1.5 Поезд начинает двигаться по прямой, параллельной оси x. Зависимость
1.1.6 Какова скорость транспортера, если за 5 с он перемещается на 10 м?
Здравствуйте. Сколько не читаю, не понятно, почему вместо радиуса надо подставлять и V0 и t0/2. Разве радиусом не будет только t0/2?
А нет, понял. Извиняюсь))
спасибо за помощь
Почему в одном случае ставим v,а другом t/2 ? Почему везде нельзя поставить v?
В таком случае у Вас ответ не получится в метрах, т.е. Вы будет ошибка в размерности. Объяснение читайте ниже в комментариях.
А почему если в качестве ответа задачи нам необходимо выяснить площадь под графиком, (которая является площадью полуокружностью) представлена площадь всего круга?
Площадь всего круга находится по формуле \(\pi r^2\), у меня же в решении \(\frac{1}{2}\pi r^2\), поэтому все верно
А смысл такого решения?
Коль S =1/2 * Pi * r^2
Не проще ли записать
S =1/2 * Pi * v0^2 = 1/2 * Pi * (t0/2)^2
???
А размерность какая у Вас получится, если будете считать по этим формулам? Правильно, м2/с2 и с2, а должно быть м.
Почитайте мой комментарий Славе, там содержится очень ценная информация.
Здравствуйте, скажите пожалуйста, а почему мы подставляем вместо первого r подставим υ0, а вместо второго – t0/2?
Можете брать наоборот, произведение от перемены мест множителей не изменится – если Ваш вопрос об этом.
Вообще эта задача интересна тем, что указанный график я могу легко из полуокружности превратить в половину овала, для этого мне достаточно взять другие единичные отрезки по любой (или по обеим осям). Хочу сказать, что полуокружность здесь получена достаточно искусственно. В таком случае площадь полуовала можно найти по формуле:\[S = \frac{1}{2}\pi ab\]Здесь \(a\) – длина малой полуоси, \(b\) – длина большой полуоси. Собственно ответ будет тот же, но никаких заморочек в объяснении здесь не возникнет.
Откуда появилось 0,25?
\(S = \frac{1}{2}\pi {\upsilon _0} \cdot \frac{{{t_0}}}{2} = \frac{1}{4}\pi {\upsilon _0}{t_0} = 0,25\pi {\upsilon _0}{t_0}\)
В графике мы видим, что начальная и последняя скорость тела равна нулю верно? Если мы разделим график на две равные части, то средняя скорость в первой и второй части будет равна v0/2, и общая средняя скорость v0/2. Теперь если мы умножим это на время, то S= (v0*t0)/2, проблема в том что наши ответы не совпадают, обЬяснити пожалуйста
Вы совершаете классическую ошибку при определении средней скорости, находя ее как разность конечной и начальной, деленной пополам. Вот только работает Ваш прием только в случае равноускоренного движения, а в этой задаче движение далеко не такое. Ведь если бы оно было таким, то график скорости от времени был бы в виде прямой, а не дуги окружности.
да вы правы, но я все сделал верно, только вот нашел ошибку, я не учел что скорость меняется не равномерно, по этому и график в форме дуги. Всего то забыл уесть что обший угол изменение графика равна п/2, тогда формула изменяется:
S=(v0*t0)/2*п/2= (v0*t0*п)/4 Все верно, и не так уж далеко от ответа))
Какой еще угол изменения графика?
Почему t0/2
тк радиус, всё понял
Радует, что Вы дошли до этой мысли сами)
Почему площадь круга, а не длина окружности?
Я решил так:
Дано:
v0 – max
t0 – all time
s – ?
Решение:
Т.к. v0 на половине времени, a1=-a2: a1=|a2|
s1+s2=s
s=v0t+(at^2)/2 (Стандартная формула без учета данных значений)
s1=(a*(1/t0)^2)/2=a/(2*t0^2) v0 стандарт. = 0; 1/t0 – 1 отрезок времени (такой же и второй)
v0=a/t0 (v0 стандартн.)
s2=a/t0*1/t0-a/(2*t0^2)= a/t0^2-a/(2*t0^2)
s=a/(2*t0^2)+a/t0^2-a/(2*t0^2)=a/t0^2
Разве так не правильно?
Ответ: s=a/t0^2
Во-первых, я не припомню, чтобы в каком-то из разделов физики длина какого-то графика имела смысл. Обычно – только площадь под графиком.
Во-вторых, s=v0t+(at^2)/2 – это формула применима только для равноускоренного движения (а оно не такое, ведь график в нашей задаче не имеет вида прямой).
Во-вторых, ускорение не дано в условии, следовательно, оно не должно фигурировать в ответе.
понял, спасибо.
но ведт по графику то видно, что тело ускоряется
Здесь есть участки, где тело ускоряется и замедляется, при этом движение точно НЕ равноускоренное и равнозамедленное