Решение: Гладкий горизонтальный диск вращается вокруг вертикальной оси с частотой

Условие задачи:

Гладкий горизонтальный диск вращается вокруг вертикальной оси с частотой 40 об/мин. От поверхности диска на расстоянии половины радиуса от оси отрывается небольшое тело, скользящее по диску без трения. Через какое время предмет соскользнет с диска?

Задача №1.8.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=40\) об/мин, \(r=\frac{R}{2}\), \(t-?\)

Решение задачи:

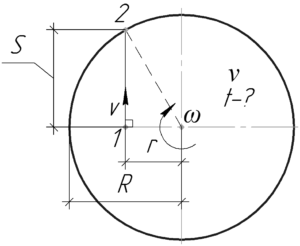В момент отрыва тело будет иметь скорость, равную линейной скорости точки диска, на которой оно находилось, то есть:

\[\upsilon = \omega r\]

Угловую скорость \(\omega\) возможно найти через частоту вращения \(\nu\) диска по формуле:

\[\omega = 2\pi \nu \]

Так как по условию \(r=\frac{R}{2}\), то скорость тела в момент отрыва определяется выражением:

\[\upsilon = 2\pi \nu \cdot \frac{R}{2} = \pi \nu R\]

После отрыва тело движется без трения, значит на него вообще не действуют никакие силы, т.е. по первому закону Ньютона оно будет двигаться равномерно и прямолинейно (от точки 1 до точки 2, смотрите рисунок). Учитывая это и пользуясь рисунком, найдем расстояние, которое пройдет тело до того как покинет диск. По теореме Пифагора:

\[S = \sqrt {{R^2} – {r^2}} = \sqrt {{R^2} – \frac{{{R^2}}}{4}} = \frac{{\sqrt 3 R}}{2}\]

Время до отрыва найдем по простой формуле:

\[t = \frac{S}{\upsilon }\]

Подставим в нее выражения для скорости тела и пути.

\[t = \frac{{\sqrt 3 R}}{{2\pi \nu R}} = \frac{{\sqrt 3 }}{{2\pi \nu }}\]

Частоту перед подстановкой в формулу необходимо перевести в систему СИ.

\[40\; об/мин = \frac{{40}}{{60}}\; об/с = \frac{2}{3}\; об/с\]

Численно искомое время равно:

\[t = \frac{{\sqrt 3 \cdot 3}}{{2 \cdot 3,14 \cdot 2}} = 0,41\; с\]