Автобус третью часть пути шел со скоростью 20 км/ч, половину оставшегося пути

Условие задачи:

Автобус третью часть пути шел со скоростью 20 км/ч, половину оставшегося пути со скоростью 30 км/ч, а остальной путь со скоростью 60 км/ч. Определить среднюю скорость на всем пути.

Задача №1.2.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_1=S_2=S_3=\frac{1}{3}S\), \(\upsilon_1=20\) км/ч, \(\upsilon_2=30\) км/ч, \(\upsilon_3=60\) км/ч, \(\upsilon_{ср}-?\)

Решение задачи:

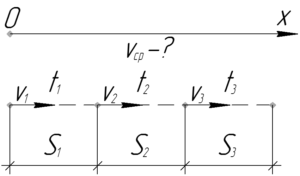Для начала прокомментируем данные задачи. В графе “Дано” мы записали \(S_1=S_2=S_3=\frac{1}{3}S\). Почему это так? Первая часть пути равна трети от всего согласно условию задачи, это сказано явно. Далее написано, что “половину оставшегося пути (он прошел) со скоростью 30 км/ч”, а половина от оставшегося, т.е. половина от \(\frac{2}{3}S\) и есть \(\frac{1}{3}S\). Значит и на последнем участке будет пройден такой же путь.

Среднюю скорость легко определить по такой формуле:

\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2} + {S_3}}}{{{t_1} + {t_2} + {t_3}}}\]

Время на прохождение любого n-ого отрезка пути равно:

\[{t_n} = \frac{{{S_n}}}{{{\upsilon _n}}}\]

Так как все отрезки равны \(S_n=\frac{1}{3}S\), то:

\[{t_n} = \frac{S}{{3{\upsilon _n}}}\]

Учитывая, что \(S_1=S_2=S_3=\frac{1}{3}S\) и написанную выше формулу, имеем:

\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{3{\upsilon _1}}} + \frac{S}{{3{\upsilon _2}}} + \frac{S}{{3{\upsilon _3}}}}}\]

\[{\upsilon _{ср}} = \frac{S}{{\frac{{S{\upsilon _2}{\upsilon _3} + S{\upsilon _1}{\upsilon _3} + S{\upsilon _1}{\upsilon _2}}}{{3{\upsilon _1}{\upsilon _2}{\upsilon _3}}}}}\]

\[{\upsilon _{ср}} = \frac{{S \cdot 3{\upsilon _1}{\upsilon _2}{\upsilon _3}}}{{S\left( {{\upsilon _2}{\upsilon _3} + {\upsilon _1}{\upsilon _3} + {\upsilon _1}{\upsilon _2}} \right)}}\]

\[{\upsilon _{ср}} = \frac{{3{\upsilon _1}{\upsilon _2}{\upsilon _3}}}{{{\upsilon _2}{\upsilon _3} + {\upsilon _1}{\upsilon _3} + {\upsilon _1}{\upsilon _2}}}\]

После всех преобразований мы получили формулу для расчета ответа.

\[{\upsilon _{ср}} = \frac{{3 \cdot 20 \cdot 30 \cdot 60}}{{30 \cdot 60 + 20 \cdot 60 + 20 \cdot 30}} = 30\; км/ч\]

Ответ: 30 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.2.4 Поезд движется на подъеме со скоростью 10 м/с, а на спуске со скоростью 25 м/с
1.2.6 Движение грузового автомобиля описывается уравнением x=-270+12t (м). Когда
1.2.7 Поезд первую половину пути шел со скоростью в 1,5 раза большей, чем вторую