Условие задачи:
Автобус прошел первые 4 км со средней скоростью 20 км/ч, а следующие 0,3 ч он двигался со средней скоростью 40 км/ч. Определить среднюю скорость на всем пути.
Задача №1.2.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=4\) км, \(\upsilon_1=20\) км/ч, \(t_2=0,3\) ч, \(\upsilon_2=40\) км/ч, \(\upsilon_{ср}-?\)
Решение задачи:
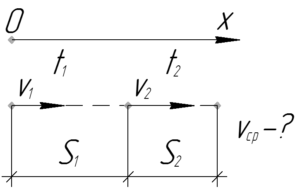Формула средней скорости автобуса на всем пути:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Движение на обоих участках пути было равномерным, поэтому:
\[\left\{ \begin{gathered}
{S_1} = {\upsilon _1}{t_1} \hfill \\
{S_2} = {\upsilon _2}{t_2} \hfill \\
\end{gathered} \right.\]
В формуле средней скорости нам неизвестно \(S_2\), мы его возьмем из второго выражения системы, и \(t_1\), его мы выразим из первого выражения.
\[{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}}\]
В итоге:
\[{\upsilon _{ср}} = \frac{{{S_1} + {\upsilon _2}{t_2}}}{{\frac{{{S_1}}}{{{\upsilon _1}}} + {t_2}}}\]
\[{\upsilon _{ср}} = \frac{{{\upsilon _1}\left( {{S_1} + {\upsilon _2}{t_2}} \right)}}{{{S_1} + {\upsilon _1}{t_2}}}\]
Остается только сосчитать ответ.
\[{\upsilon _{ср}} = \frac{{20 \cdot \left( {4 + 40 \cdot 0,3} \right)}}{{4 + 20 \cdot 0,3}} = 32\; км/ч = 8,9\; м/с\]
Ответ: 8,9 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.12 Мотоциклист за первые 5 минут проехал 3 км, за последующие 8 минут – 9,6 км и
1.2.14 Какое расстояние пробежит конькобежец за 40 с, если он будет двигаться
1.2.15 Вагон, двигаясь под уклон, проходит 120 м за 10 с. Скатившись с горки, он проходит
Я все никак не могу понять,как из предпоследней формулы,выходит v1(s1+v2t2)/s1+v1t2,я так понял это свойство дробей,понимаю глупый вопрос,но все объясните,если не сложно
Легко, имеем:\[{\upsilon _{ср}} = \frac{{{S_1} + {\upsilon _2}{t_2}}}{{\frac{{{S_1}}}{{{\upsilon _1}}} + {t_2}}}\]У нас в знаменателе одной дроби появилась другая дробь, работаем сначала с ней:\[\frac{{{S_1}}}{{{\upsilon _1}}} + {t_2} = \frac{{{S_1} + {\upsilon _1}{t_2}}}{{{\upsilon _1}}}\]По сути у нас такой случай:\[{\upsilon _{ср}} = \left( {{S_1} + {\upsilon _2}{t_2}} \right)/\left( {\frac{{{S_1} + {\upsilon _1}{t_2}}}{{{\upsilon _1}}}} \right)\]Из математики известно, что:\[a/\frac{b}{c} = a \cdot \frac{c}{b} = \frac{{ac}}{b}\]Отсюда и получим:\[{\upsilon _{ср}} = \frac{{{\upsilon _1}\left( {{S_1} + {\upsilon _2}{t_2}} \right)}}{{{S_1} + {\upsilon _1}{t_2}}}\]
Короче говоря, мы в знаменателе дробь приводим под общий знаменатель, когда это сделаем, знаменатель этой дроби отправляется в числитель другой дроби.\[{\upsilon _{ср}} = \frac{{{S_1} + {\upsilon _2}{t_2}}}{{\frac{{{S_1} + {\upsilon _1}{t_2}}}{{{\upsilon _1}}}}}\]
\[{\upsilon _{ср}} = \frac{{{\upsilon _1}\left( {{S_1} + {\upsilon _2}{t_2}} \right)}}{{{S_1} + {\upsilon _1}{t_2}}}\]
Почему в последней формуле написано V1, а не Vср?
Потому что опечатка) Спасибо за замечание!
Рад помочь)
Спасибо ! Лучший сайт по физике
почему в предпоследней формуле в знаменателе остается v1
Я получил эту формулу, умножив числитель и знаменатель формулы выше на v1.
Из s1 и v1 находим t1 а из t2 и v2 находим s2 и наконец все это ставим в формулу υср=S1+S2/t1+t2 это второй способ;)
Вы решили задачу не в общем виде, Вам необходимы промежуточные вычисления.
В идеале Вы должны получить одну формулу, в которой нет неизвестных величин, а лишь данные задачи, физические постоянные и табличные величины.